Study Notes on Correlation and Regression || Commerce || Management || Economics
By BYJU'S Exam Prep
Updated on: September 13th, 2023

Table of content
Correlation
A person can confine himself to the univariate distributions, i.e. distributions based on only one variable. However, one may come across two or more variables simultaneously. For example, Height -weight; Advertisement-Sales; Income and expenditure; Price and demand; Price and supply, etc.
Also, one can be interested to find out if there is any correlation between the two variables in the consideration. There can be the following possibilities of correlation between variables:
- Both the variables change in the same direction [if one variable increases (or decreases), another variable also increases (or decreases)]
- Both the variables change in opposite direction [if one variable increases (or decreases) other variable decreases (or increases )]
Thus, the types of correlation are as follows:
- If both the variables change in the same direction then the correlation is said to be a positive correlation and
- If they change in the opposite direction then the correlation is said to be a negative correlation.
- Correlation is said to be perfect if the deviation in one variable is followed by a corresponding and proportional deviation in the other.
There are two methods to compute the correlation coefficient
Scatter diagram; and Karl Pearson coefficient of correlation
1. Scatter diagram
If the values of the variables X and Y are plotted along the x-axis and y-axis respectively in the xy plane, the diagram of dots obtained is known as the scatter diagram.
From the scatter diagram, we can get a good idea
- If dots are very dense then we can assume a strong correlation between these two variables
- If the dots are scattered all over the plane then there is poor correlation between these two variables plotted on xy plane
This method has some disadvantages:
- This method is not suitable if the number of observation is large
- This method is not able to give a numeric value of the correlation
2. Karl Pearson coefficient of correlation
As a measure of the degree of the linear relationship between two variables, Karl Pearson developed a formula called Karl Pearson coefficient of correlation.
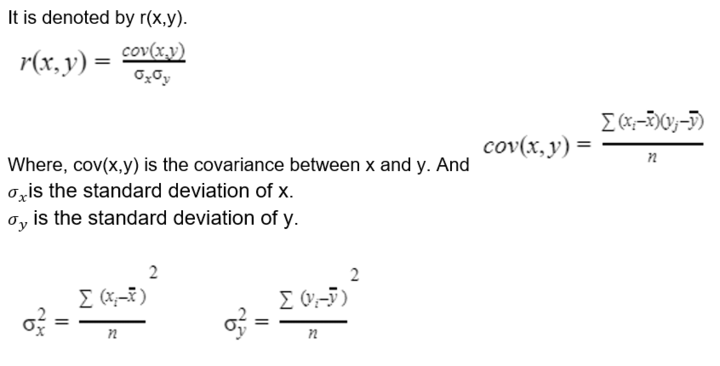
Properties of the correlation coefficient
- It is independent of change of order and change of origin i.e. if u=x-h/a , v=x-k/b then r(x,y)=r(u,v)
- Limit of r(x,y) is -1 to 1
- r(x,y) only provides a measure of the linear relationship between these two variables; it is not suitable for non-linear relation.
- Two independent variables are uncorrelated as for independent variable cov(x,y)=0.
- Two uncorrelated variables (zero correlation and zero covariance) are not independent.
- Zero correlation implies linear independence.
The probable error of the correlation coefficient
If r is the sample correlation coefficient in a sample of n pairs of observations, then it’s the standard error

The reason for taking the factor 0·6745 is that in the normal distribution, the range 1.1 ± 0·6745 covers 50% of the total area.
Rank Correlation
- Let us take a group of n individuals arranged in order of merit or proficiency in possession of two characteristics A and B. These ranks in the two characteristics will, in general, be different. For
- example, if we consider the relation between intelligence and power. It is not necessary that a powerful individual is intelligent also. Let (Xi. Yi); i = 1, 2, …, n be the ranks of the ith individual in two characteristics A and B respectively.
- Pearsonian coefficient of correlation between the ranks Xi's and Yi's is called the rank correlation coefficient between A and B for that group of individuals.
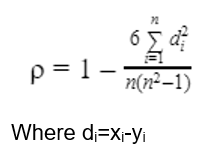
Notes:
- Spearman’s rank correlation is nothing but the Karl Pearson coefficient of correlation between the ranks so it can be interpreted in the same as Karl Pearson coefficient of correlation.
- Spearman’s rank correlation is easy to calculate compared to the Karl Pearson coefficient of correlation.
- While dealing with qualitative data, Spearman's correlation coefficient should be used.
Regression Analysis
- Regression analysis is a measure of the average measure of the relationship between two variables.
- It means “Stepping back towards the Average”.
- In regression analysis, there are two types of variables
- Which is influenced or is to be predicted by another variable called dependent variable (regressed, explained).
- Which influences another variable called the independent variable (regressor, predictor and explanatory).
- Let us take a set of bivariate data, let’s say x and y. So if x and y are related then we will find that the points in the scatter diagram will cluster round some curve called the "curve of regression". If the curve is a straight line we call it “line of regression”.
- The line of regression is the line that gives the best estimate to the value of one variable for any specific value of the other variable. Thus the line of regression is the line of "best /it" and is obtained by the principles of least squares.
- Let x is an independent variable and y is a dependent variable and (xi,yi) are the n observations of x and y.
- And the line of regression on y on x is, y=a+bx
- a is called intercept term and b is called slope term.
- According to the principle of least squares, for estimating a and b we have following two equations, these are called normal equations

Properties of Regression
- In a particular case of perfect correlation, positive or negative, i.e., r ± I, the equation of the line of regression of Y on X becomes the equation of the line of regression of X on Y.
- The correlation coefficient is the geometric mean between the regression coefficients,
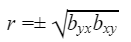 the sign to be taken before the square root is that of the regression coefficients.
the sign to be taken before the square root is that of the regression coefficients.
- If one of the regression coefficients is greater than unity, the other must be less than unity.
- The arithmetic mean of the regression coefficient is greater than the correlation coefficient r, provided r>0.
Mock tests for UGC NET Exam
UGC NET Online Coaching
Thanks.
Score better. Go BYJU'S Exam Prep.


