Shear Flow: Definition and Formula
By BYJU'S Exam Prep
Updated on: September 25th, 2023
The topic of shear flow frequently occurs when dealing with built-up beams. Shear flow is used in both solid mechanics and fluid dynamics. The shear flow is used to indicate the shear stress over a distance in a thin-walled structure.
In solid mechanics, the shear flow comes into the picture when a transverse force is applied over a cross-section of the beam and it represents the variation of shear stress along the cross-section of the beam.
Table of content
What Is Shear Flow
Shear flow is a term that is used in solid mechanics and in fluid dynamics both. The general expression for shear flow is used to represent shear stress along the distance of a particular cross-section in a thin-walled shell or any structure. Shear flow is also defined as the flow which is induced by an external force.
Variation of the shear flow at a given cross-section can also be expressed by equation VQ/I. This equation is simply the value of the multiplication of shear stress and the thickness of the member.
Shear Flow Definition
Shear flow is defined as the longitudinal shear force which is transmitted per unit length of the beam across the plane. In the case of the thin-walled shell, shear stress along the face of the structure can be termed as the shear flow because variation over thickness can be neglected.
Representation of shear flow in an I-Section:
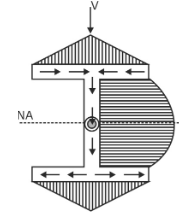
Shear Flow In Thin-Walled Sections
The thin-walled section is basically a section having less thickness. Thin-walled sections don’t have a solid cross-sectional area. Cross section of such beams is generally made up of thin panels which are connected with each other.
Shear flow is just the flow of shear force along the cross-section of a member. In the case of thin-walled sections, shear flow is the flow of shear force per unit length of the perimeter of the thin-walled section.
The Shear Flow Based On Elastic Behavior
Shear flow is a term that is significant for a cross-section of a member for a particular structural member. So, it will depend on the cross-sectional properties of the member as well as it depends on the material properties of the member and it also depends on the value and type of external loads.
Shear flow in a particular cross-section affects the cross-sectional dimensions of a structure. Based on the elastic behavior of members deformation of the cross-section will occur. Shear flow can be calculated as shear force per unit distance along the cross-section.
Shear Flow And Shear Centre
Shear flow: It is the flow of shear force along the unit length along the cross-section. It affects the cross-sectional dimension of the member which depends upon the geometrical properties and cross-sectional properties of the member.
Shear Centre: It is the point within or outside the body of the member for which there is no twisting over the section if loads pass to this point. The direction of shear flow depends on the position of the shear center of the member
Shear Stress And Shear Flow
Shear stress is the stress acting on the cross-section of a beam or structure. It is calculated by the shear force per unit area. It has a unit of N/mm2. It is maximum at the neutral axis and zero at the top most and bottom most fiber.
Shear flow is the flow of shear force along the length of a section. It is calculated as shear stress multiplied by the thickness of the member. It depends on the geometrical properties of the cross-section.
Related Important Links
| Fixed Beams | Solid Mechanics |
| Moment Of Inertia | Proof Resilience |
| Modulus Of Rigidity | Mohr’s Circle |
| Shear Force | Strain Gauge |
| GATE Civil Syllabus | GATE 2023 login |


