Shear Centre Formula, Definition and examples
By BYJU'S Exam Prep
Updated on: September 25th, 2023
The shear center is a point within or outside the structure on which, if loads are acting, it will cause no twisting to the cross-section. The centroid is the point where total body weight acts. It can be the same in some cases but not in all situations.
The position of the shear center depends upon the geometry of the section and other dimensions of the member. It can be simulated as the centroid of a system of internal shear force. There is only bending on the system if a load passes through it.
What is Shear Centre?
The shear centre is defined as the point about which the external load must be applied to produce no twisting moment across the cross-section of the structural member. Loads must be applied at a particular point in the cross-section, called the shear centre if the beam is to bend without twisting. The shear centre is a point on which, if load acts; there will be no twisting of the cross-section, which means that only bending and direct stresses will act on the section. In general, it differs from the centroid of the body. The position of the shear centre will depend on the cross-sectional parameters.
The shear centre of the cross-section may differ from the centroid of the cross-section. And the distribution of the shear stress across the section depends on the geometry of the section and other cross-sectional parameters. The resultant of the shear stress for a particular cross-section acts on the point of the shear centre of the section. For a doubly symmetric cross-section, the shear centre and centroid of the section will coincide. The transverse load will result in a bending moment and twisting moment for a beam if it is not applied at the shear centre, but if it is applied on the shear centre, then it will only cause a bending moment to the cross-section.
Shear flow in the cross-section of the body governs by the position of the shear centre. Shear flow is the variation of shear stress along the section of the body, which helps to find the shear force acting on a particular section. Hence overall shear flow is an important parameter of designing the structural member.
Download Civil Engineering Short Notes for Fluid Mechanics
Definition Of Shear Centre
An enteral centre is where a shear force can act without producing any twist in the sectionnter. In such conditions, only bending stresses will act over the section.
Download Formulas for GATE Civil Engineering – Solid Mechanics
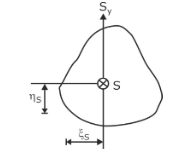
Location of Shear Centre
The shear centre for a member is the point at which, if the load is applied, it will cause no twisting to the centre. The location of the shear centre can be found by equating the moment due to external force to the total resisting moment for a particular section. Here a general expression for a section is explained below with the help of the following diagram.



