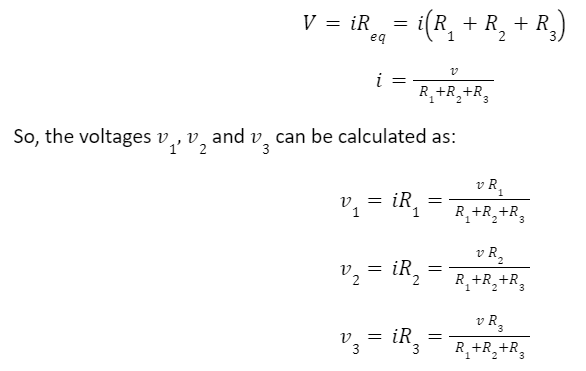Resistors in Series

Resistors in Series

Resistors are said to be in series connection when the current across all the resistors is the same, and the voltage across the individual resistor is different. Although if all the resistors in series have the same resistance, then the voltage across each resistor will also be the same.

Resistors in series are used as a resistance voltage divider circuit. Also, resistors in series distribute the heat occurring due to power dissipation among resistors, thus doesn’t load the circuit.

Need for Series Combination of Resistors

When the same current flows through the resistors and the potential developed across the resistors is different, the combination is said to be a series combination of resistors. If a fault occurs on any one of the resistors in the circuit, the entire circuit will get affected or turned off. Resistors in series can be modeled as shown below:

Resistors are connected in series for the following purposes:

• Increase the effectiveness or overall resistance.
• Divide the potential V between all the resistors to get a small value of potential.
• Resistors in series spread the heat dissipation and thus won’t load the circuit.

Download Formulas for GATE Electronics & Communication Engineering – Digital Circuits

Equivalent Resistance of Resistors in Series

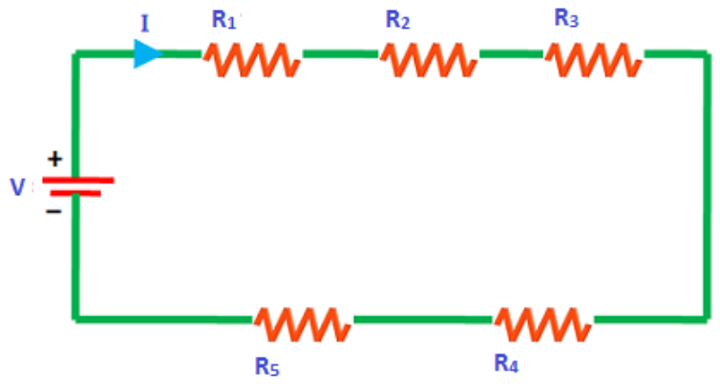
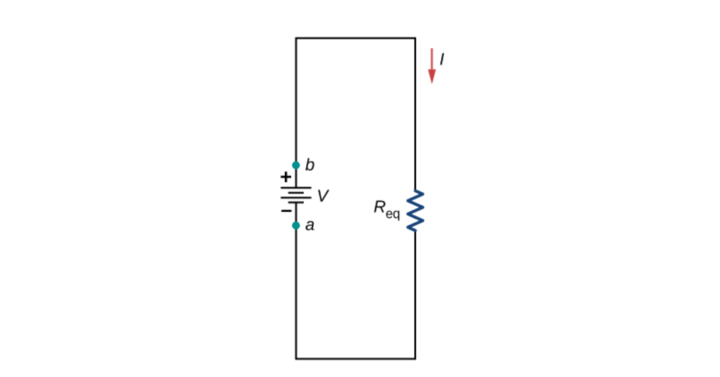
For simplification, let us calculate the equivalent resistance for the two resistors connected in series as shown below:

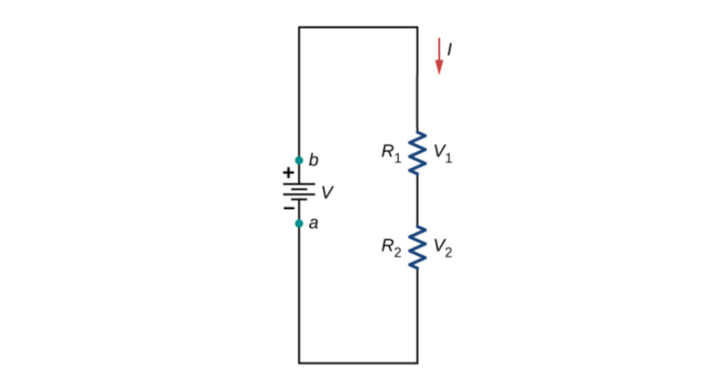
In the above circuit, the same current i flows through the resistors R₁ and R₂. If R₁≠R_2, then v₁≠v₂.

From Ohm’s law,

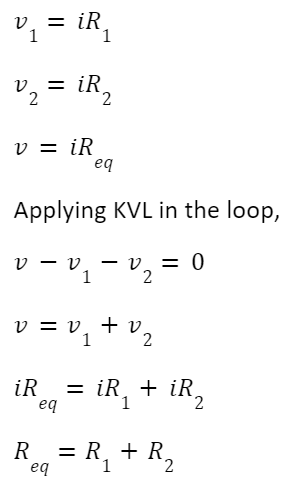
Where R_eq is the effective resistance of the circuit and can be modelled as:

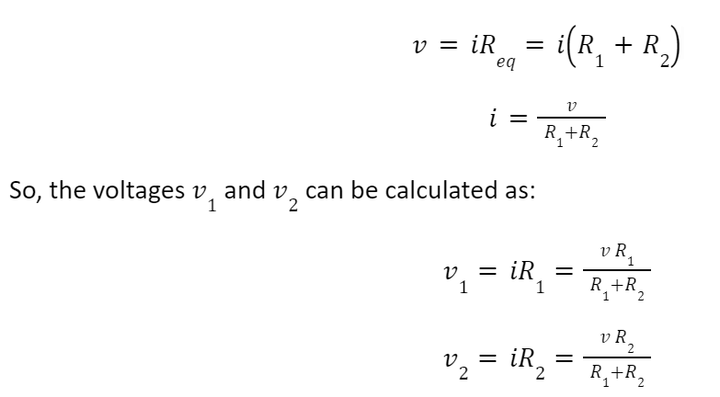
The source voltage v is divided between R₁ and R₂. This is known as the principle of voltage division.

Similarly, let us calculate the equivalent resistance for the three resistors connected in series as shown below:

 

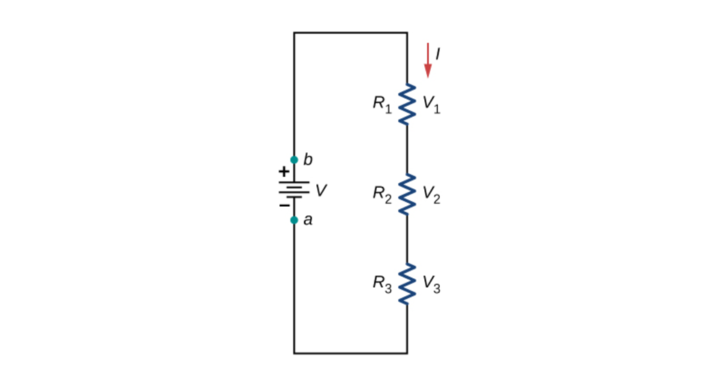
Let v₁ be the voltage drop across resistor R₁

Let v₂ be the voltage drop across resistor R₂

Let v₃ be the voltage drop across resistor R₃

From Ohm’s law,

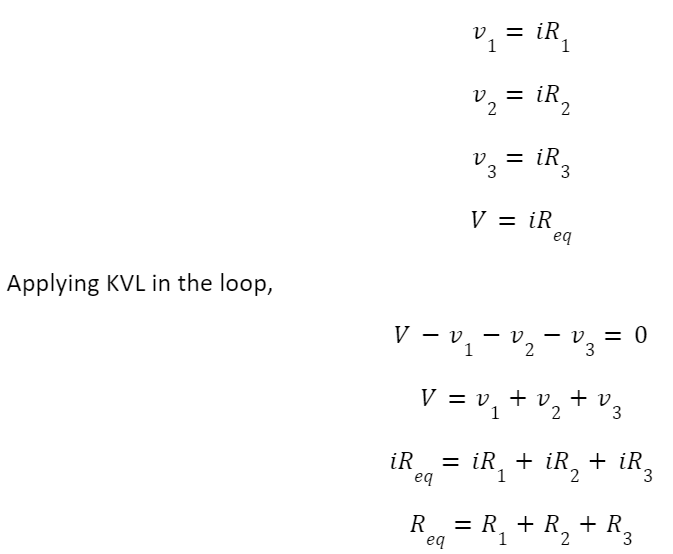
Where R_eq is the effective resistance of the circuit where we connected resistors in series and can be modeled as:

Download Formulas for GATE Electronics & Communication Engineering – Electronic Devices

Resistors in Series Formula

When N a number of resistors are connected in series then the overall equivalent resistance is the sum of individual resistance connected in the circuit. Mathematically, resistors in the series formula can be written as:

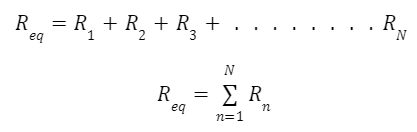
Similarly, the voltage across any resistor connected in series can be calculated as:

V_n = VR_n/ R_eq

Resistors in Series Examples

Example 1: Find the source current I from the figure shown below:

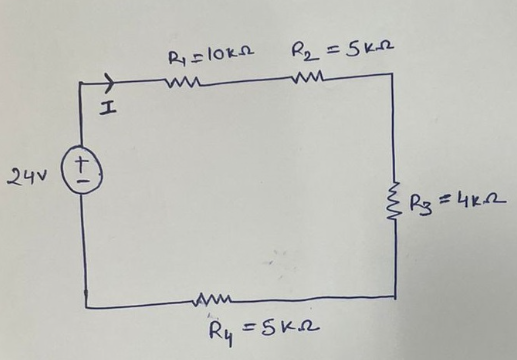
Solution: From the above circuit, the current is the same across all the resistors, so resistors are in series. The above circuit can be modeled as an equivalent resistance circuit as shown below:

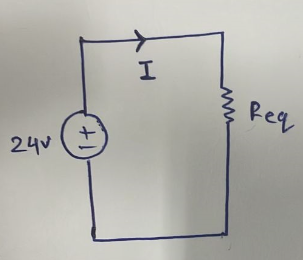
Req =R₁+R₂+R₃+R₄ = 10 + 5+4+5=24 kΩ

So, from ohm’s law,

I=V/R_eq =24 V/24kΩ = 1 mA

Example 2: Find the equivalent resistance seen from the terminal ab and the voltage across each resistor in the circuit shown below:

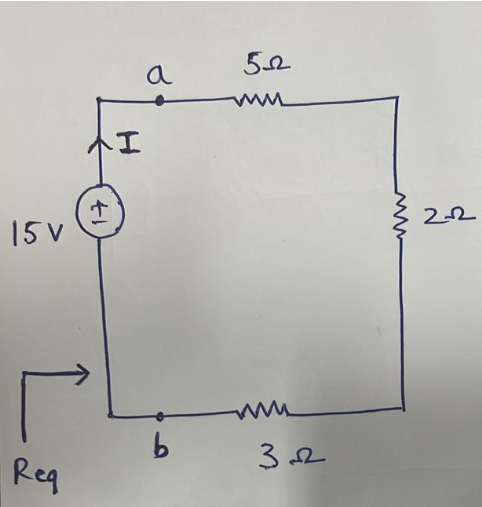
Solution: From the figure, resistors are in series so that the equivalent resistance can be calculated as,

Difference Between Resistors in Series and Parallel

In brief, the difference between resistors in series and resistors in parallel is shown below in tabular form based on certain parameters. Let V_n be the voltage across the resistors and in the current across the resistors.

Parameters	Resistors in series	Resistors in parallel
Definition	When there exists only a path of current to flow, and source voltage divides across the resistors with the same current across all resistors.	When there exists multiple paths of current to flow and current divides across the resistors with the same voltage across all resistors.
Source Voltage V	Source voltage gets divided between all the resistors in series. V=V1+V2+V3 . . . . Vn	Source voltage appears across each resistor in parallel. V=V1=V2=V3=… =Vn
Source Current I	Source current only flows from each resistor in series. I=I1=I2=I3=. . . =In	Source current gets divided between all the resistors in parallel. I=I1+I2+I3 . . . . In
Voltage across resistors	Different if all resistors have different resistance. Same if all resistors have the same resistance.	Always the same irrespective of the resistance value.
Current across resistors	Always the same irrespective of the resistance value.	Different if all resistors have different resistance. Same if all resistors have the same resistance.
Equivalent Resistance	The equivalent resistance is greater than all the resistance present in the circuit. Req=R1+R2+R3+ . . . . . . Rn	The equivalent resistance is always less than the smallest resistance present in the circuit. 1/Req=1/R1+1/R2+1/R3+ . . . . . . 1/Rn

 

Important GATE Topics
Fixed End Moment	Gravity Of Earth
Slope Deflection Equation	Capacitors in Parallel
Capacitors in Series	Carnot Cycle
Cement Test	Clamping Circuit
CMOS Converter	Column Base