Maxwell’s Reciprocal Theorem
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In designing the structure, there are a few parameters that need to be known before the start of the design process. These are called design parameters, consisting of maximum bending moment, maximum shear force and deflection, etc. And to find out the maximum deflection under any combination of loads, Maxwell’s reciprocal theorem can be used.
Maxwell’s Reciprocal Theorem is based on the effect of loads on the material and is used to find the deformation or deflection in beams. Maxwell’s reciprocal theorem can also determine the deflection in trusses or frames. In this article, we will understand everything related to this theorem.
Table of content
What is Maxwell’s Reciprocal Theorem?
Maxwell’s reciprocal theorem is used in structural analysis to find the deflection at any point in the structure. With the help of this theorem, we can relate the deflection of two different points of the same beam under a combination of loads. For structural analysis, Maxwell’s reciprocal theorem can be applied to beams.
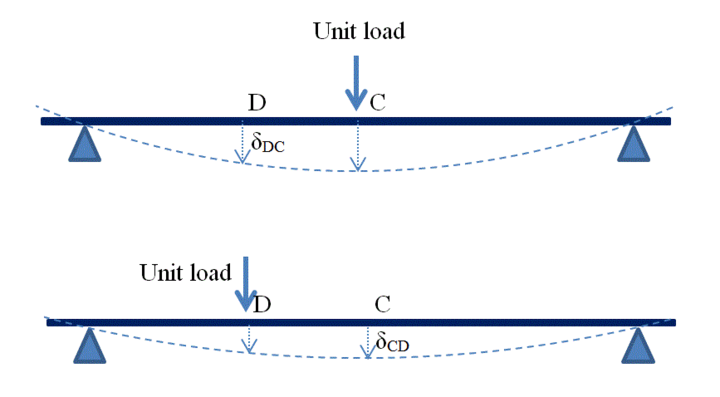
State Maxwell’s Reciprocal Theorem
Maxwell’s reciprocal theorem states that the deflection of point C due to load at point B is equal to the deflection of point B due to load at point C. As in this theorem, two different beam points are considered for analysis, and properties (deformation) are the same when loads are reversed among these two points. Due to this reversibility nature, this theorem is called Maxwell’s reciprocal theorem.
Download Formulas for GATE Civil Engineering – Environmental Engineering
Maxwell’s Reciprocal Deflection Theorem
It is a basic structural engineering tool that relates distortions at two different points in the elastic structure, like beams and frames. Maxwell’s reciprocal deflection theorem is also known as Maxwell’s reciprocal rule. It establishes a technical relationship between deflection and point load applied to the elastic structure. It equates to distortions at two different points in the elastic structure when it is alternatively subjected to the same at these points. This theorem can also be used to verify the solution of equations used to calculate the deflection at two different points.
Maxwell’s reciprocal deflection theorem is an extension of Betti’s law which states that deflection at one point due to unit load at the other point is equal to the deflection at another point due to unit load at a first point in the beam.
Maxwell’s Reciprocal theorem is based on the principle of virtual work, which states that work done by the external forces in the structure is equal to the work done by the internal forces under the same structure conditions.
Download Formulas for GATE Civil Engineering – Fluid Mechanics
Maxwell’s Reciprocal Theorem Application
Maxwell’s reciprocal theorem can be applied to beams having the same cross-sectional area along their length. And hence we can say that Maxwell’s reciprocal theorem applies to prismatic beams.
Maxwell’s reciprocal theorem in structural analysis can also be applied in the case of non-prismatic members, but it should follow Hooke’s law.
With the help of this theorem, we can find the flexibility coefficient matrix to solve the compatibility equations for analyzing the indeterminate structure. Moreover, this theorem and Betti’s law also help to draw the influence line diagram in the case of indeterminate structures.
Explain Maxwell’s Reciprocal Theorem
As we know that Betti’s theorem establishes the relationship between deflection and point load in the beam. So it can be said that this law explains Maxwell’s reciprocal theorem. To better understand Maxwell’s reciprocal theorem, consider a beam subjected to a point load, as shown in the figure.
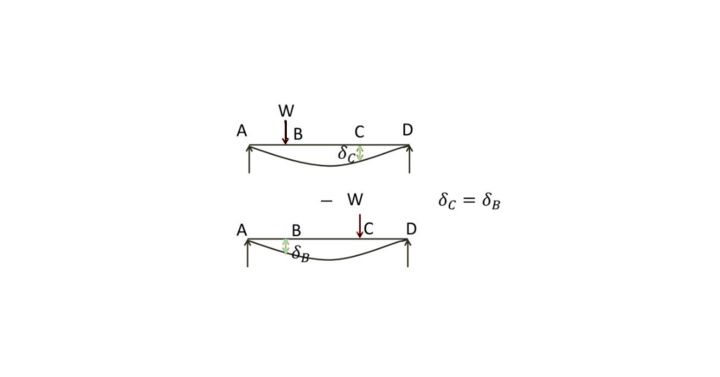
Let W at point B is applied gradually first, which produces a deflection of b at B and a deflection of δc at C, as shown in the figure.
So, work done=1/2Wb
When W is applied at C, it will produce a deflection c at C and an additional deflection δB at B.
So, extra Work done=1/2Wc+WδB
Hence, total work done=1/2Wb+1/2Wc+WδB
Similarly, if the loads were applied in reverse order and the load W at C produced an additional deflection at B, then.
Total Work done=1/2Wb+1/2Wc+Wδc
And deflection should be the same at any point regardless of the order of application of load. It should depend on where the load is being applied first. So total work done in both cases is equal hence.
WδB=Wδc
So, δB= δc
Maxwell’s Reciprocal Theorem and Betti’s Theorem
Maxwell’s reciprocal theorem and Betti’s theorem are based on the principle of virtual work, and Maxwell’s theorem is a special case of Betti’s theorem. Enrico Betti discovered Betti’s theorem in the year 1872. According to this theorem, work caused by a set of forces through the displacement caused by the other set of forces is equal to the work done by the other set of forces through displacements at the point of the first set of forces. This theorem has many applications in structural engineering. For example, this theorem also helps to define the influence line diagram of a beam or structure. Furthermore, Betti’s theorem uses a topology optimization approach to solve complicated structural engineering problems.
And in Maxwell’s reciprocal theorem, there is only one load in both sets of loads, as described in Betti’s theorem. These changes in this theorem are a special case of Betti’s theorem. Both the theorems, which are explained in terms of displacements and point loads, can also be explained in terms of moment and rotation in the structure. Thus rotation at one point in the structure due to a unit moment at some other point is equal to the rotation at another point due to a unit moment at the first point.
Maxwell’s Reciprocal Theorem Uses
Maxwell’s reciprocal theorem is related to the displacement and point load applied to the beams. It also has many applications related to any linearly elastic body and surfaces. We can also use this theorem for finding rotations of torques applied in the body. Torques. It is derived relatively straightforwardly by examining the work when two different forces are applied. Understanding of this theorem will be clear by solving the questions.
Maxwell’s reciprocal rule is one of the basic rules of structural engineering, which relates to the deformation and point load acting in the body. It also relates to the rotation and moments acting in the body. It can be used to reduce the calculation for finding the displacement in the structure in complex loading conditions over the structure. And it also can be used to cross-verify the calculation used to determine the deflection.


