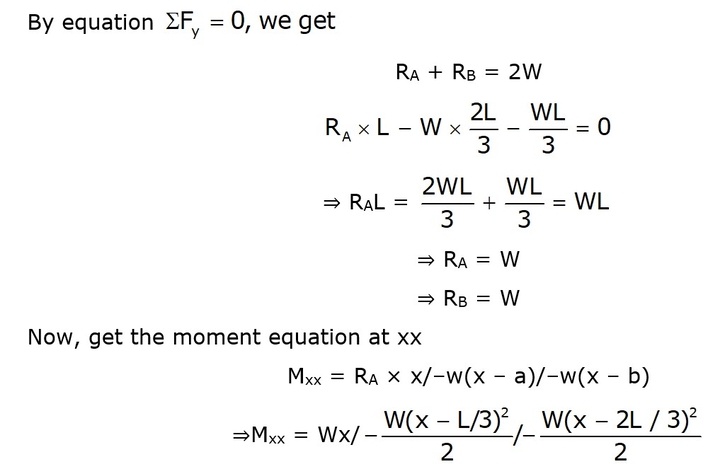Macaulay's Method

What is Macaulay’s Method?

Macaulay’s method is suitable for prismatic beams containing concentrated loads and moments. In such cases, bending moment equations change from one part to the other part of the span of the beam.

Macaulay’s method is an improvement over the double integration method in which the most generalized bending moment equation is written in a specific format, as given below.

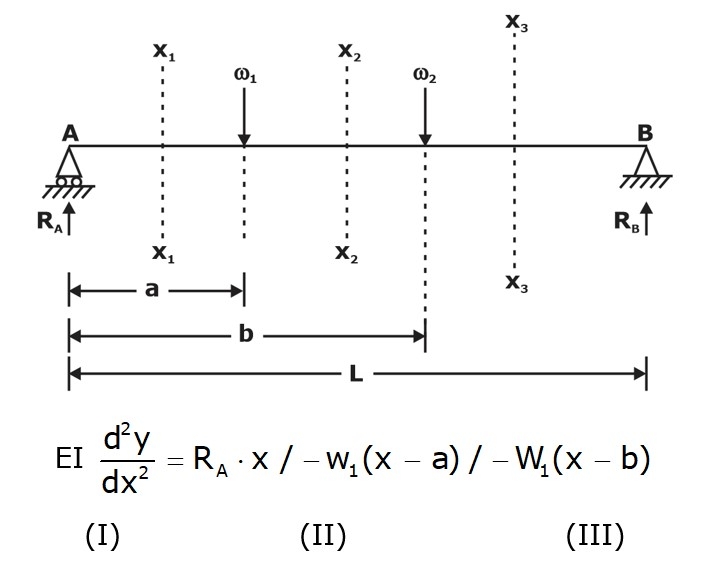
The oblique (/) sign indicates that the successive terms may be and may not be valid;

For example: If 0≤x≥a, then only the I^st term is valid.

If b≤x≥L, then all terms are valid.

On integrating the above equation, we can get the slope and deflection equation of the beam.

The integration of Macaulay’s equation is in a specific form:

(i) The constants of integration C₁ and C₂ are added after the I^st term

(ii) The integration of (x-a) and (x-b) is done as (x-a)²/2 and (x-b)²/2, respectively.

(iii) To determine constants C₁ and C₂, the conditions are applied for slope and deflection when end conditions are applied, then only valid terms and accounted for.

When Macaulay's Method is Preferred?

As we know, Macaulay's method is used to determine the slope and deflection of the beam. This method is the simplest version of the double integration method for finding the deflection. The double integration method is also used to calculate the slope and deflection of the beam. The double integration method is easier when there is no variation in loading intensity over the beam. In such cases, only one bending moment equation is required to write for the whole beam to calculate the slope and deflections. For example, if only a uniformly distributed load is applied on the whole span of the beam, then only one bending moment equation is sufficient for the whole span of the beam.

Macaulay’s method is preferred over the double integration method when variation in loading intensity occurs over the beam's span. It is also an important part of the GATE CE syllabus. Because in the case of Macaulay’s method, the bending moment equation of all the spans can be written simultaneously. For example, Suppose point load, uniformly distributed load, or any other load combination is applied on a beam. In that case, the bending moment equation can be written in one form, as described earlier. And this equation can be used based on the span.

Macaulay's Method for Slope and Deflection

In structural analysis, as per the GATE exam, various methods are available for finding the slope and deflection of beams. The use of all those methods depends on the suitability of the methods and loading conditions over the span. Different methods for finding the slope and deflection are mentioned below:

• Double Integration Method
• Macaulay's Method
• Conjugate Beam Method
• Moment Area Method
• Strain Energy Method

Macaulay’s method is the Simplification of the double integration method. The Conjugate beam method is used in complex loading conditions; It converts the real beam into a conjugate beam by changing its supports such that the deflection and slope of the real beam are equal to the bending moment and shear force of the conjugate beam, respectively. The moment area method is mainly used for the beam having non-prismatic sections, but it can also be used for prismatic sections. And strain energy method for calculating the slope and deflections of the beams is based on the concept of strain energy. It uses Castigliano’s theorem to calculate these parameters.

Macaulay’s Method for Cantilever Beam

Macaulay’s method is based on the double integration concept for finding the slope and deflection of the beam. Macaulay’s method is more convenient for beams carrying a different combination of loads because, in such cases, only one bending moment equation is sufficient for finding slope and deflection for the whole span of the beam. Finding the slope and deflection of the beam will depend on the loading intensity and the beam type.

In the case of a cantilever beam, finding the deflection and slope of the beam also depends on the type of loading applied over it. So considering the uniformly distributed load over the beam, 1^st calculate the bending moment equation. Then by integrating it twice, the defection of the beam at a point can be determined.

Example of Macaulay’s Method

Macaulay’s method becomes important when loading conditions and its type change over the whole span of beams. Various NAT-based questions can be formulated in this method in the GATE question paper. This method's concept becomes clearer by solving a numerical problem of calculating the slope and deflections with the help of this method. Here such an example is shown, which helps to understand this method in a better way.

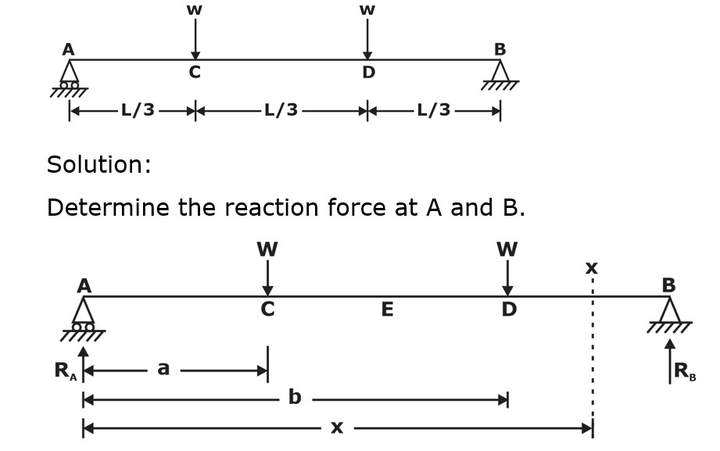
Example: Find the slope at A and B and the deflection at the center of the beam using Macaulay’s method.