Knapsack Problem Using Greedy Method
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Knapsack Problem Using Greedy Method: The selection of some things, each with profit and weight values, to be packed into one or more knapsacks with capacity is the fundamental idea behind all families of knapsack problems. The knapsack problem had two versions that are as follows:
- Fractional Knapsack Problem
- 0 /1 Knapsack Problem
The fractional Knapsack problem using the Greedy Method is an efficient method to solve it, where you need to sort the items according to their ratio of value/weight. In a fractional knapsack, we can break items to maximize the knapsack’s total value. This problem in which we can break an item is also called the Fractional knapsack problem. Here, we will see Knapsack Problem using Greedy method in detail, along with its algorithm and examples.
Table of content
What is Knapsack Problem Using Greedy Method?
In this method, the Knapsack’s filling is done so that the maximum capacity of the knapsack is utilized so that maximum profit can be earned from it. The knapsack problem using the Greedy Method is referred to as:
Given a list of n objects, say {I1, I2,……, In) and a knapsack (or bag).
The capacity of the knapsack is M.
Each object Ij has a weight wj and a profit of pj
If a fraction xj (where x ∈ {0…., 1)) of an object Ij is placed into a knapsack, then a profit of pjxj is earned.
The problem (or Objective) is to fill the knapsack (up to its maximum capacity M), maximizing the total profit earned.
Mathematically: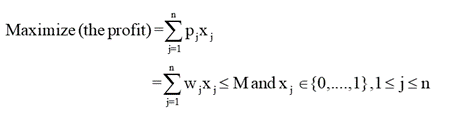
Note that the value of xj will be any value between 0 and 1 (inclusive). If any object Ij is completely placed into a knapsack, its value is 1 (xj = 1). If we do not pick (or select) that object to fill into a knapsack, its value is 0 ( xj = 0). Otherwise, if we take a fraction of any object, then its value will be any value between 0 and 1.
Knapsack Problem Algorithm Using Greedy Method
Knapsack Problem Using Greedy Method Pseudocode
A pseudo-code for solving knapsack problems using the greedy method is;
greedy fractional-knapsack (P[1…n], W[1…n], X[1..n]. M)
/*P[1…n] and W[1…n] contain the profit and weight of the n-objects ordered such that X[1…n] is a solution set and M is the capacity of knapsack*/
{
For j ← 1 to n do
X[j]← 0
profit ← 0 // Total profit of item filled in the knapsack
weight ← 0 // Total weight of items packed in knapsacks
j ← 1
While (Weight < M) // M is the knapsack capacity
{
if (weight + W[j] =< M)
X[j] = 1
weight = weight + W[j]
else{
X[j] = (M – weight)/w[j]
weight = M
}
Profit = profit + p[j] * X[j]
j++;
} // end of while
} // end of Algorithm
Knapsack Problem Using Greedy Method Example
We have thoroughly discussed the fractional knapsack problem and the algorithm for the knapsack problem using Greedy method. Now to understand it better, let us see an example.
Consider the knapsack instances, the capacity of the knapsack is 15, and 7 object has profit and weight as follows:
|
Object |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
Weight |
2 |
3 |
5 |
7 |
1 |
4 |
1 |
|
Profit |
10 |
5 |
15 |
7 |
6 |
18 |
3 |
Which object is partially placed in the knapsack using the fractional knapsack problem?
- X4
- X2
- X1
- X3
Answer: Option B
Solution: Let us first find each object’s profit by weight ratio.
|
object |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
Profit/weight |
5 |
1.66 |
3 |
1 |
6 |
4.5 |
3 |
Now we will arrange the profit by weight ratio in descending order and pick the objects accordingly.
|
X5 |
X1 |
X6 |
X7 |
X3 |
X2 |
|
6 |
5 |
4.5 |
3 |
3 |
1.6 |
The total capacity of the knapsack = 15
After selecting X5 capacity = 15-1=14
After selecting X1 capacity = 14-2=12
After selecting X6 capacity = 12-4=8
After selecting X7 capacity = 8-1=7
After selecting X3 capacity = 7-5=2
After selecting X2 capacity = 2-(2/3)*3=0
Thus we are taking only 2/3rd weight of the object X2
We take fractional parts from X2.
Therefore, option B is correct.


