Kinematic Indeterminacy

What is Kinematic Indeterminacy?

Kinematic Indeterminacy is the term associated with Indeterminate structures. It can be defined as the Minimum number of dimensions in which movement is allowed for the structure. These structure movements are also called the Degree of Freedom of structure. And these movements of the structure are independent of each other.

Kinematic Indeterminacy can also be determined with the help of kinematic unknowns, and these unknowns are the joint movements and movement of the end member of the structure. These kinematic unknowns can be found with the help of the structure’s compatibility conditions and equilibrium equations.

Formulas for GATE Civil Engineering – Fluid Mechanics

Kinematic Indeterminacy Formula

As we know, kinematic Indeterminacy is the number of degrees of freedom associated with the structure members. So, we can calculate its value by calculating the Degree of freedom of all the members and joints of a structure. The Degree of freedom of a member depends upon whether the member is axially extensible or not because if the member is axially rigid, it means it can not move in the axial direction and hence reduces the one Degree of freedom of that particular member.

To establish the kinematic indeterminacy formula for a member or a structure, calculate the Degree of freedom of all the associated members and subtract the Degree of freedom that is prevented by constraints like supports, internal hinges, etc. While for the calculation of the Degree of static Indeterminacy, support reactions are used. The indeterminate kinematic structure shows the kinematical rigidness of the structure.

Download Formulas for GATE Civil Engineering – Environmental Engineering

Degree of Kinematic Indeterminacy

The Degree of kinematic Indeterminacy is the total number of independent degrees of freedom available in the structure. It also can be determined by the number of unrestrained directions in which structural movements are allowed. And we can determine the Degree of static Indeterminacy only by deducting the number of equilibrium equations from the support reactions.

The Degree of kinematic Indeterminacy for a rigid framed structure can be calculated as D_K=3J-R_e. Where J is the number of joints in the rigid frame and R_e is the number of total external reactions in the structure. At the same time, the Degree of static Indeterminacy for a planar structure can be calculated as D_s=R-3 where R is the total number of support reactions present in the structure.

Download Formulas for GATE Civil Engineering – Fluid Mechanics

Difference Between Static and Kinematic Indeterminacy

Static and kinematic Indeterminacy are both types of Indeterminacy and tells about the redundant reactions and Degree of freedom of structure and hence can be used to estimate the stability of the structure. Though the stability of the structure is a different thing, somehow, we can relate it with the Indeterminacy of the structure.

Static Indeterminacy is the number of support reactions over the equilibrium equations available, or we can say that it equals the number of redundant reactions. There are only three numbers of equilibrium equations available for a 2D structure and 3D analysis; there are six numbers available that are used to find the Degree of static Indeterminacy of the structure. But if we talk about kinematic Indeterminacy, it is equal to the number of degrees of freedom available in the structure. And degrees of freedom are the number of directions in which structures can move freely without restrictions.

Kinematic Indeterminacy For Propped Cantilever Beam

As we know, kinematic Indeterminacy is the number of degrees of freedom available in the whole structure where a structure can move. So, Before finding the Indeterminacy, we need to know how many directions a propped cantilever beam can move freely. Hence it is important to know whether the member of a propped cantilever beam is axially extensible or not because it restricts the axial movement of the beam, and the Degree of freedom will be affected.

So, it is now considered that the member of the propped cantilever beam is not axially-extensible, which means the member can not move axially. Now, we need to understand the support conditions of the propped cantilever beam. So propped cantilever beam has fixed support at one end and roller support at the other. As we know, fixed support does not allow movement in any direction, and roller support only restricts movement in the vertical direction of the beam, but as we consider beam is inextensible. Hence, movement in the axial direction of the beam is also not possible, and only rotation is allowed about its point. So, the Degree of freedom of fixed support is zero, and for roller support, it is only one in this beam condition. Hence, the overall Degree of freedom for this condition of the propped cantilever beam is only one.

Kinematic Indeterminacy For Propped Cantilever with Axial Deformation

As we know, kinematic Indeterminacy is the number of degrees of freedom in the structure. So, Before calculating the Indeterminacy, we need to know how many directions a propped cantilever beam can move freely. So, if the member of the propped cantilever beam is axially deformable, the beam can move axially if allowed.

So, As in this case, the propped cantilever beam is axially deformable, which means the member can move axially. Now, we need to understand the support conditions of the propped cantilever beam. So propped cantilever beam has fixed support at one end and roller support at the other. As we know, fixed support does not allow movement in any direction, and roller support only restricts movement in the vertical direction of the beam. So we can say that the roller support of the beam can provide movement in the axial direction and rotation and only constraint in the vertical direction of the beam. So, the Degree of freedom of fixed support is zero; for roller support, it is only two in this beam condition. Hence, the overall Degree of freedom for this condition of the propped cantilever beam is only two.

Degree of Kinematic Indeterminacy for Truss

Each plane truss joint has two independent displacement components that will translate along the x-y direction. So, we can often write the Degree of kinematic Indeterminacy (or Degree of freedom) for a plane truss can as 2j – R, where R is the number of compatibility conditions known.

As all the members of a truss system are considered to be extensible (or axial deformation is taken into account for every truss), the boundary conditions( value of R) are going to be obtained only from support conditions are going to be equal to the number of reaction forces(r). Hence, a plane truss’s Degree of kinematic Indeterminacy is adequate to 2j – r.

Kinematic Indeterminacy Examples

Kinematic Indeterminacy can be calculated by knowing the total Degree of freedom associated with the structure. And we also know the formula for solving the kinematic Indeterminacy. Here some examples are given below to find out the kinematic Indeterminacy of the structure, which helps to understand the whole concept.

1. Find the Kinematic Indeterminacy of the bridge structure given below.

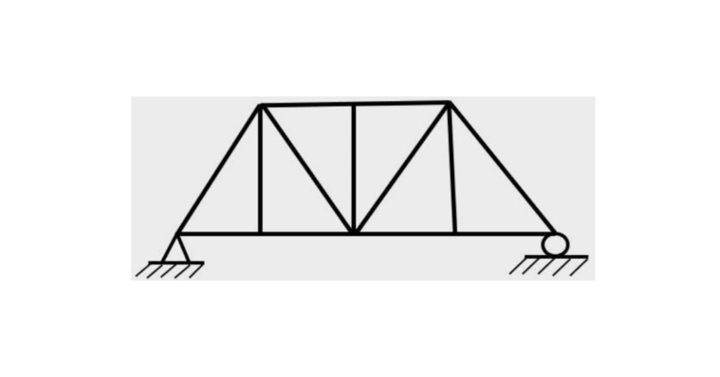
The degree of kinematic indeterminacy for above structure = 2j – R = 2*8 – 3 = 13 Ans.

2. Find the Kinematic Indeterminacy of the extensible structure given below.

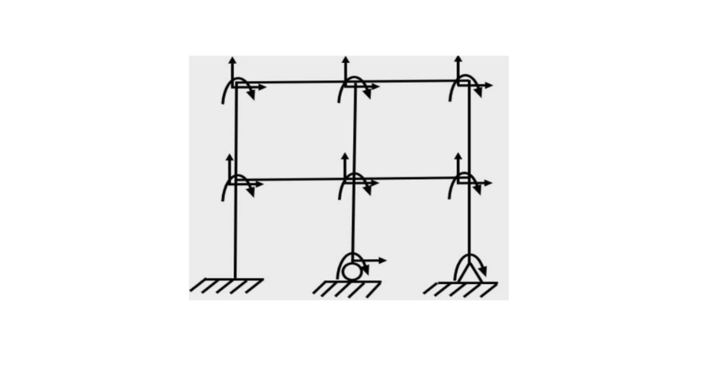
For calculating the kinematic Indeterminacy, it is assumed that all members of this frame are extensible,

Hence, the degree of kinematic indeterminacy = 3j – R = 3*9 – 6 = 21.

Important GATE Topics
Lan Full Form	Propped Cantilever Beam
Torsional Force	POP Full Form
RTC Full Form	Fcfs Scheduling Full Form
Types Of Loads	E-Commerce Mcq
Laser Full Form	Rankine Formula