Ideal Rankine Cycle

What is Rankine Cycle?

The Rankine cycle is used for analyzing the changes in working substances in steam turbine power plants. Heat is supplied to the working substance so that it can produce some amount of work.

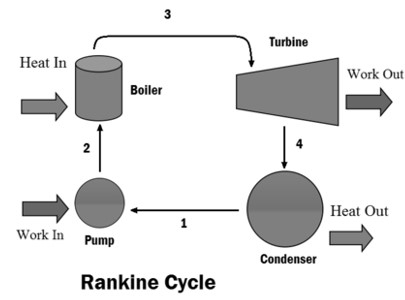
Figure: Rankine Cycle

Q_s amount of heat is supplied to the boiler then water converted into steam, this high thermal energy steam passes through nozzle then this high-velocity stream impinging the turbine blade so that turbine produces W_T amount of work then it passes through the condenser, Q_R amount of heat rejected from the steam so that steam is converted into water then this water pumped into the boiler by using a hydraulic pump. W_P amount of work input is required to run the pump.

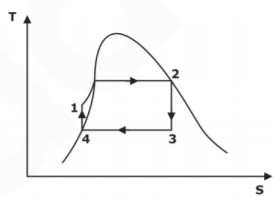
Figure: Rankine Cycle

• Process 2-3: Isobaric Heat Transfer:
  High-pressure liquid enters the boiler from the feed pump (1-2) and is heated to the saturation temperature (2). Further addition of energy causes evaporation of the liquid until it is fully converted to saturated steam (3).

• Process 3-4:Isentropic Expansion:
  The vapor is expanded in the turbine, thus producing work that may be converted to electricity. In practice, the expansion is limited by the temperature of the cooling medium and by the erosion of the turbine blades by liquid entrainment in the vapour stream as the process moves further into the two-phase region. Exit vapour qualities should be greater than 90% to avoid blade erosion.

• Process 4-1:Isobaric Heat Rejection:
  The vapour-liquid mixture leaving the turbine (3-4) is condensed at low pressure, usually in a surface condenser using cooling water. In well-designed and maintained condensers, the pressure of the vapour is well below atmospheric pressure, approaching the saturation pressure of the operating fluid at the cooling water temperature.

• Process 1-2:Isentropic Compression:
  The pressure of the condensate is raised in the feed pump. Because of the low specific volume of liquids, the pump work is relatively small and often neglected in thermodynamic calculations.

  Work done on the pump, per kg of water: W_P= h₂ – h₁

  Energy added in steam generator: q₁= h₃ – h₂

  Work delivered by turbine: W_T= h₃ – h₄

  Energy rejected in the condenser, q₂ =h₄ – h₁

• The thermal efficiency of the Rankine cycle is given by:
  

Ideal Rankine Cycle

A steam turbine power plant consists of a boiler, turbine, condenser and pump. Reversible isobaric heat addition (1-2) takes place in the boiler then the steam passes through the nozzle and high-velocity steam is impinging the turbine blades. Reversible adiabatic expansion or isentropic expansion (2-3) takes place in the turbine. Steam is allowed to pass into the condenser and reversible isobaric heat rejection (3-4) takes place in the condenser. Steam is converted into the water in a condenser and water is pumped into the boiler by using a hydraulic pump. Reversible adiabatic pumping (4-1) takes place in the pump.

h-s and T-s Diagram for Ideal Rankine Cycle

As we discussed above, reversible isobaric heat addition (1-2) takes place in a boiler, reversible adiabatic expansion or isentropic expansion (2-3) in a turbine, reversible isobaric heat rejection (3-4) in the condenser and reversible isentropic pumping (4-1) in the heat pump. The h-s and T-s diagrams for the ideal Rankine cycle are shown in Fig. below.

Efficiency of Ideal Rankine Cycle

The efficiency of the ideal Rankine cycle is defined as the ratio of net work done by the steam turbine power plant W_netand heat supplied to the boiler Q_s. The difference between turbine workout W_T and pump work input W_p is defined as net work done W_net.

The procedure to determine the expression for efficiency of the ideal Rankine cycle is given below.

The process (1-2): reversible isobaric heat addition (Boiler)

Amount of heat supplied in the boiler:

Apply S.F.E.E

h₁+Q_s=h₂

Q_s=h₂-h₁

The process (2-3): reversible adiabatic expansion (isentropic expansion) (turbine)

Amount of work done by the turbine:

Apply S.F.E.E

h₂=W_T+h₃

W_T=h₂-h₃

The process (3-4): reversible isobaric heat rejection (Condenser)

Amount of heat rejected in condenser:

Apply S.F.E.E

h₃=Q_R+h₄

Q_R=h₃-h₄= h₃-h_f4

The process (4-1): reversible adiabatic pumping or isentropic pumping (Pump)

Amount of work input in pump:

Apply S.F.E.E

h₄+W_P=h₁

W_p=h₁-h₄=h₁-h_f4=v_f4(P_b-P_c)

Net work done in steam turbine power plant:

W_net = W_T-W_P=(h₂-h₃)-(h₁-h_f4)

The efficiency of the Rankine cycle

η_Rankine=Net Work Done/Heat Supplied

η_Rankine=W_net/Q_s=[(h₂-h₃)-(h₁-h_f4)]/h₂-h₁