Huffman Coding – Algorithm, Tree, Example, Methods, Encoding
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Huffman Coding is a greedy technique to obtain an optimal solution to a problem. The Huffman coding is generally used for lossless data compression mechanisms. Sometimes, it is also called data compression encoding. It makes sure that there is no ambiguity while decoding the output bitstream.
Greedy algorithms use a heuristic approach to make an optimal choice at each stage while problem-solving to find a globally optimized solution. Before learning the Huffman coding algorithm, we will first see the greedy design technique, followed by the Huffman coding algorithm meaning and an example for better understanding.
Download Formulas for GATE Computer Science Engineering – Programming & Data Structures
Table of content
What is Huffman Coding?
The Huffman coding is widely used in data compression techniques. It is used for both encoding and decoding. It uses a greedy approach to solve problems. The greedy approach allows us to solve a problem and find an optimal solution using the optimal substructure. An optimal substructure to a problem is achieved if an optimal solution can be created from the optimal solutions of its subproblems.
The Huffman coding uses a prefix rule that avoids ambiguity while decoding. The two steps involved in Huffman coding are:
- Construct a Huffman tree from the input string or text or characters.
- Assigning a Huffman code to each character by traversing the tree.
Download Formulas for GATE Computer Science Engineering – Algorithms
Huffman Coding Algorithm
The Huffman coding algorithm, as already discussed, follows the greedy design approach to arrive at an optimal solution. It uses a Huffman tree to encode and decode the data. A Huffman tree is created using the following steps:
- Create a leaf node for each character of the text.
- Arrange all the nodes in the increasing order of their frequency.
- Considering the first two nodes have the minimum frequency.
-Create an internal node.
-The frequency of this internal node is the sum of the frequency of the previous two nodes.
-Make the first and second nodes the left and right children respectively of the newly created node. - Repeat steps 2 and 3 until all the nodes form a tree. The tree thus obtained is a Huffman tree.
After the Huffman tree is created, each character is assigned a unique code. For decoding, the same Huffman tree is traversed.
Download Formulas for GATE Computer Science Engineering – Digital Logic
Applications of Huffman Coding
We have thoroughly discussed the Huffman coding approach (Greedy Design Technique) and its algorithm. Now let us see the applications of the Huffman coding mechanism, which are as follows:
- It is applied where a series of frequently occurring characters are used.
- Used for transmitting the data in the form of text or fax etc.
- Used by conventional compression formats like GZIP, PKZIP, etc.
- Multimedia formats like JPEG, PNG, and MP3 use Huffman encoding.
Huffman Coding Example
We will see an example to understand how we should approach solving a problem using the Huffman code.
Question: Consider the following message: ppqqrrsspqrsprrsss?
Find the number of bits required for Huffman coding?
Answer: 36.
Solution:
Frequencies: p-4 , q-3 , r-5 , s-6
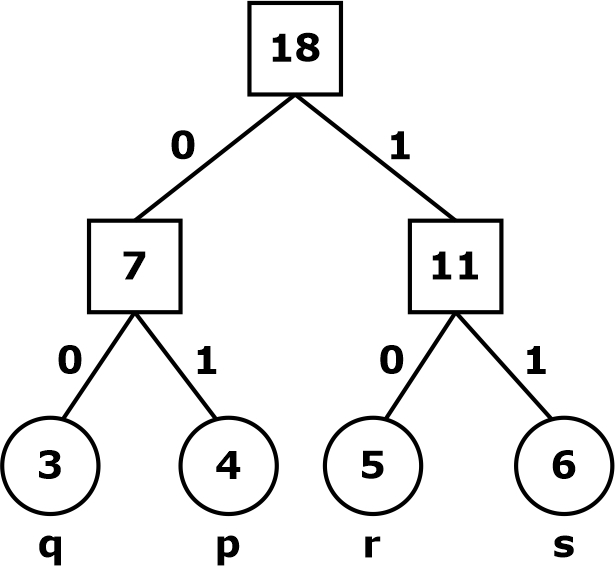
p – 01, q – 00, r – 10, s – 11
The total bits required for Huffman coding is
∑ (frequency) x (bits) = 4(2) + 3(2) + 5(2) + 6(2) = 36


