Geometric Design of Highways
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Geometric Design of Highways is an important concept of highway design. In the design of highway engineering, various elements of roads are designed, like cross-sectional dimensions, longitudinal slope, transverse slope, etc. The geometric design of highways includes the parameters like sight distances, horizontal and vertical curves, etc.
Geometric Design of Highways PDF
The geometric design of highways deals with designing the parameters related to the aspects of visible features of the roads. The geometric design of highways should be such that it ensures the factor of safety for the road and the driver. It also considers the comfort parameters of vehicles and passengers traveling in vehicles. This article discusses various features of the geometric design of highways in detail.
Table of content
-
1.
What is the Geometric Design of Highways?
-
2.
Highway Cross Section Elements and Geometric Design of Highways
-
3.
Factors Affecting the Geometric Design of Highways
-
4.
Different Sight Distances Used in Geometric Design of Highways
-
5.
Horizontal Alignments in Geometric Design of Highways
-
6.
Various Curves in the Geometric Design of Highways
What is the Geometric Design of Highways?
The geometric design of highways is one of the parameters of designing highways, including various sight distances, cross-sectional elements, etc. Geometric designing is important part of the GATE CE syllabus and includes determining various layouts and visible features of the highways. Features of the geometric design of highways also include gradients and intersections on highways.
The geometric design of highways should be such that it ensures the requirements of the driver for traveling on highways, and it also ensures the safety criteria with the comfort condition of the driver. Hence, it ensures the overall efficiency of the road in terms of its design. The geometric design of highways can be affected by the characteristics of traveling vehicles, the driver’s behavior, the interrelationship between driver and traffic characteristics, total traffic volume, and speed.
Highway Cross Section Elements and Geometric Design of Highways
The geometric design of highways consists of many parameters like cross-sectional elements, sight distances, gradients, intersections, etc., which are essential for the GATE exam. Sigh distances can be of many types, like stopping sight distance, overtaking sight distance, headlight sight distances, intermediate sight distance, etc. These sight distances are explained further in this article.
Cross-sectional elements come under the geometric design of highways; it includes road width of pavement, transverse superelevation, shoulder, etc. Cross-sectional elements of a road affect the characteristics of the road and riding comfort and safety. Pavement characteristics include friction, unevenness, drainage, and other parameters. These cross-section parameters play an important role in the geometric design of highways.
Factors Affecting the Geometric Design of Highways
The geometric design of highways includes various parameters, including designing a cross-sectional element, Designing for the various sight distances, design for various curves, etc. These highway parameters will depend on traffic velocity, road characteristics, user characteristics, etc. The geometric design of highways will depend upon various factors like vehicle characteristics, the psychology of the driver, Traffic volumes, traffic characteristics etc. Here are some factors are given that affect the geometric design of highways:
- Vehicle behaviour
- Human behaviour
- Environmental factors
- Economical factors
- Traffic conditions
- Topography factors
- The design speed of the road
The road’s design speed will govern the design of the sight distances, horizontal, vertical, etc. Design speed for a road section is generally taken as the 85th percentile speed. Topography factors are one of the main important parameters of designing highways. It is considered important because in the case of flat terrain cost of construction is less, and it becomes more in the case of hilly terrain. So, it can be said that the topography of a terrain indirectly affects the economy of the whole project.
Different Sight Distances Used in Geometric Design of Highways
Sight Distance is the distance that is necessary to visible for the driver, It can be classified as Stopping sight distance and Overtaking sight distance; based on the requirements of the road; these distances are explained below:
Stopping Sight Distance (SSD)
The minimum sight distance available on a highway at any spot should be of sufficient length to stop a vehicle traveling at the designed speed safely without collision with any other obstruction. Therefore, the absolute minimum sight distance is equal to the stopping sight distance, also sometimes called non-passing sight distance. The MSQ questions can be formulated based on the stopping sight distance in the GATE question paper.
The stopping distance of a vehicle is the sum of the following:
- The distance traveled by the vehicle during the total reaction time is known as lag distance and
- The distance traveled by the vehicle after applying the brakes to a dead stop position is known as the braking distance.

Overtaking Sight Distance (OSD)
The minimum distance open to the vision of the driver of a vehicle intending to overtake a slow vehicle ahead with safety against the traffic of opposite direction is known as the minimum overtaking sight distance (OSD) or the safe passing sight distance available
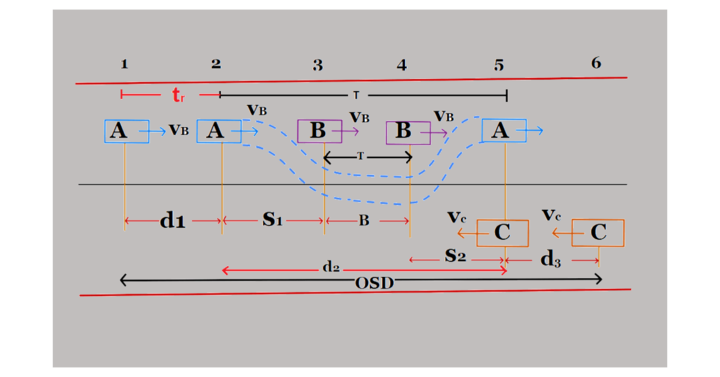
OSD = d1+d2+d3
Where O.S.D = Overtaking sight distance in ‘m’
d1 = Distance traveled by overtaking vehicle A during the reaction time t sec of the driver from position 1 to position 2 as described in the figure. It is assumed that in this region, the overtaking vehicle travels with the speed of a slow-moving vehicle.
d1 = 0.278 Vb t
d2 = Distance traveled by vehicle A from position 2 to Position 5 during the actual overtaking operation in time T sec.

d3=0.278VCT
Where,
- d3 = Distance traveled by oncoming vehicle C from position 6 to position 5 during the overtaking operation of A, i.e., T sec.
- VC = V = Speed of overtaking vehicle or design speed (km/hr)
If Vb is not given, then It can be assumed that;
Vb = (V-16)km/hr
Vb = (V-4.5)m/s
v = design speed in m/s.
Overtaking Zone
It is desirable to construct highways so that the length of the road visible ahead at every point is sufficient for safe overtaking. This is seldom practicable, and there may be stretches where the safe overtaking distance cannot be provided. In such zones were overtaking or passing is not safe or is not possible, signposts should be installed indicating “No passing” or “Overtaking Prohibited” before such restricted zones start. But the overtaking opportunity for vehicles moving at design speed should be given at frequency intervals. These zones, which are meant for overtaking, are called overtaking zones.
For one-way traffic overtaking sight distance = d1+d2
For two-way traffic overtaking sight distance= d1+d2+d3

Minimum length of overtaking zone = 3(OSD)
The desirable or maximum length of overtaking zone = 5(OSD)
Horizontal Alignments in Geometric Design of Highways
Alignments are one of the important parameters in the geometric design of highways. These alignments can be classified as horizontal alignment and vertical alignment. Here some horizontal alignments of geometric design are described.
Super Elevation(e)
To counteract the effect of centrifugal force and reduce the vehicle’s tendency to overturn or skid, the outer edge of the pavement is raised concerning the inner edge, thus providing a transverse slope throughout the length of the horizontal curve. This transverse inclination to the pavement surface is known as the cant or superelevation.
The superelevation ‘e’ is expressed as the ratio of the height of the outer edge to the horizontal width.

Maximum Super Elevation (emax):
| Type of Terrain | Superelevation |
| Plain and rolling | 0.07 |
| Hilly terrain | 0.10 |
| For urban roads | 0.04 |
Extra Widening (EW): The extra pavement widening on horizontal curves is divided into two parts (i) Mechanical and (ii) Psychological widening.
Mechanical Widening (Wm): The widening required to account for the off-tracking due to the rigidity of the wheelbase is called mechanical widening.
Psychological widening (Wp): Extra width of the pavement is also provided for psychological reasons, such as to provide for greater maneuverability or steering at higher speeds, to allow for the extra space requirements for the overhangs of vehicles, and to provide greater clearance for crossing and overtaking vehicles on the curves. Psychological widening is therefore important in pavements with more than one lane.
![]()
Where
n = number of traffic lanes
l = length of wheelbase (m)
R = radius of the curve (m)
V = velocity (kmph)
Various Curves in the Geometric Design of Highways
Curves are required for the smooth transition of the direction of vehicles. As per the GATE notes, these curves can be classified into vertical curves and horizontal curves. These are explained below:
Transition Curve
The transition curve is the curve having an infinite radius at its straight end, and it gradually reduces to the curve radius at the point of tangency of the curve.
The Indian Roads Congress recommends the use of the spiral as a transition curve in the horizontal alignment of highways due to the following reasons:
The spiral curve satisfies the requirements of an ideal transition.
The geometric property of a spiral is such that the calculations and setting out the curve in the field is simple and easy.
Length of Transition Curve (L)
(i) According to the rate of change of radial/centrifugal acceleration
L=0.0215 V3/CR
Where;
- V = Speed of vehicle in (km/hr)
- C = Allowable rate of change of centrifugal acceleration in m/sec3
- C=80/(75+V)
- R = Radius of the curve in ‘m’.
- L = Length of the transition curve in ‘m’.
(ii) According to the rate of change of the super-elevation length of the transition curve can be calculated as follows:
| Length | Type of Terrian |
| 150 X | Plain and rolling terrain |
| 100 X | For built-up area |
| 60 X | For hilly area |
Where X = Raise of the outer line of the road.
X = (w + Ew)e; If pavement is rotated about inner side.
X = (w + Ew)e/2; If the pavement is rotated about the center line.
(iii) According to the empirical formula (rate of change of curvature)
L=2.7 V2/R; For plain and rolling terrain
L=V2/R; For hilly area
Set Back Distance (m)
The clearance distance or set back distance required from the center line of a horizontal curve to an obstruction on the inner side of the curve. It is provided for adequate sight distance. And it depends upon the following factors:
(i) Required sight distance (SSD)
(ii) Radius of the horizontal curve, (R)
(iii) Length of the curve (Lc)
Grade Compensation
Grade compensation is provided on the curve to make the smooth traveling of vehicles because, on the curves, some loss occurs in tractive force due to the change in the direction of vehicles. The percentage reduction in grade compensation is calculated by the minimum (30+R)/R and 75/R. And compensated grade should not be less than 4%
Where R = Radius of the curve in meters.
Vertical Curve
Due to changes in grade in the vertical alignment of the highway, it is necessary to introduce a vertical curve at the intersections of different grades to smoothen out the vertical profile and thus ease off the changes in gradients for the fast-moving vehicles.
The vertical curves used in highways may be classified into two categories:
(i) Summit curves or crest curves with convexity upwards
(ii) Valley or sag curves with concavity upwards.
- Summit Curves (Crest Curve with Convexity Upward): Summit curves are curves that have convexity in the upward direction. The deviation angles between the two interacting gradients equal their algebraic difference. Among all the cases, the deviation angle will be maximum when an ascending gradient meets with a descending gradient, i.e., N = n1 – (-n2) = (n1 + n2)

(i) Length of summit curve for SSD
(a) when L > SSD
L=NS2/4.4
Where
- L = Length of summit curve in meter
- S = SSD (m)
- N = Deviation angle= Algebraic difference in grade
- H = Height of eye level of the driver above roadway surface = 1.2 m
- h = Height of object above the pavement surface = 0.15 m
(b) When L < SSD
L=2S – 4.4/N
(ii) Length of summit curve for safe overtaking sight distance (OSD) or intermediate sight distance (ISD)
(a) When L > OSD
L=NS02/9.6
Where S0 = Overtaking or Intermediate sight distance
(b) When L < OSD
L=2S0 – 9.6/N
- Valley Curves (Sag Curve with Concavity Upward): Valley curves or sag curves are formed in any of the cases illustrated in fig. In all the cases, the maximum possible deviation angle is obtained when a descending gradient meets with an ascending gradient.

(i) Length of valley curve as per comfort condition (transition curves are provided back to back).
L=0.38 (NV3)1/2 if C=0.6 m/sec3
(ii) Length of valley curve for headlight sight distance (parabolic curve is provided).
(a) When L > SSD
L= NS2/(2h1+2s tanα) ⇒ L= NS2/(1.50+0.035s)
Where,
- L = Total length of valley curve
- S = SSD (m)
- N = Deviation angle
- α = Beam angle ∼ 1°
- h1 = Avg. height of headlight = 0.75 m
(b) When L < SSD
L=2S – (2h1+2s tanα)/N ⇒ L= 2S – (1.50+0.035s)/N
Here, you can find a detailed design of the vertical curve and related concepts in the following video, which strengthens your concept related to the geometric design of highways. For other related concepts, stay tuned with the Byju Exam Prep official youtube channel:


