Flow Through Pipes: Major and Minor Losses in Flow Through Pipes

Q: What do you mean by flow through pipes?

Flow through pipes means the study of the flow characteristics when it occurs in a pipe. During the flow through pipes, an external source of energy is always required to flow because in such conditions flow is occurring under the energy gradient.

Q: Which type of flow is possible during the flow through pipes?

During the flow through pipes, flow can be laminar type, turbulent type, or transition type of flow. These flows can be classified based on the Reynolds number of the flow, which depends on the flow and pipe characteristics.

Q: What are the different types of losses occured in the flow through pipes?

Losses can be classified as major and minor during the flow through pipes. Major losses occurred in the pipe flow due to friction occurring at the wall of the pipes. And minor losses occur due to sudden contraction, expansion, exit, entrance, etc.

Q: What do you mean by flow through parallel pipes?

In the case of flow through parallel pipes, head loss occurs between both ends of the flow is the same for the different parallel combinations of pipes. In such conditions of flow through pipes, total discharge is the sum of the discharges through the different pipes.

Q: What are the different minor losses occured during the flow through pipes?

Minor losses occurred in the flow through pipes consisting of loss due to sudden contraction, loss due to sudden expansion, entrance loss, exit loss, etc. these losses have less contribution to the total loss occurred in the flow.

What is Flow Through Pipes?

Flow through pipes is an important topic in fluid mechanics. It is important to understand the different types of losses that occur during the flow through pipes for the GATE CE exam. Based on different losses, the total energy at the exit point of the pipe is calculated.

Major Losses in Flow Through Pipes

In flow through pipes, losses that occur in the pipe flow are a very important parameter for the design. These losses include the major loss due to friction and some minor losses. Darcy Weisbach's equations can calculate major losses in flow through pipes. These are explained as follows.

Loss of head due to friction

h_f = 4fLv²/2gd

where,

L = Length of pipe,
v = Mean velocity of flow
d = Diameter of pipe,
f = Coefficient of friction

or h_f = f'Lv²/2gd

f' = 4f

friction factor for laminar flow, f = 64/ R_e

Coefficient of friction, f = 16/ R_e

For turbulent flow, the coefficient of friction

f = 0.079/(R_e)^0.25

Chezy’s Formula: In fluid dynamics, Chezy’s formula describes the mean flow velocity of steady, turbulent open channel flow.

v= c √mi, c= Chezy's Constant = √(8g/f)

Relation between Coefficient of Friction and Shear Stress

We get

f = 2τ₀/ρv²

where,

f = Coefficient of friction
τ₀ = Shear stress

Minor Losses in Flow Through Pipes

Another type of head loss, minor loss, is induced for the following reasons. These losses are used in the GATE CE question paper to create the NAT-based questions.

Loss due to Sudden Enlargement

Head loss, h_L = (v₁ - v₂)²/ 2g

Loss due to Sudden Contraction

Head loss, h_L = 0.5 v₂²/ 2g

Remember, v₂ is the velocity at a point in the contracted section.

Loss of Head at Entrance to Pipe

Head loss,

h_L = 0.5V²₁/2g

Loss at Exit from Pipe

Head loss,

h_L = V²₁/2g

Combination of Pipe Connections

Pipes may be connected in series, parallel or in both. Let's see their combinations.

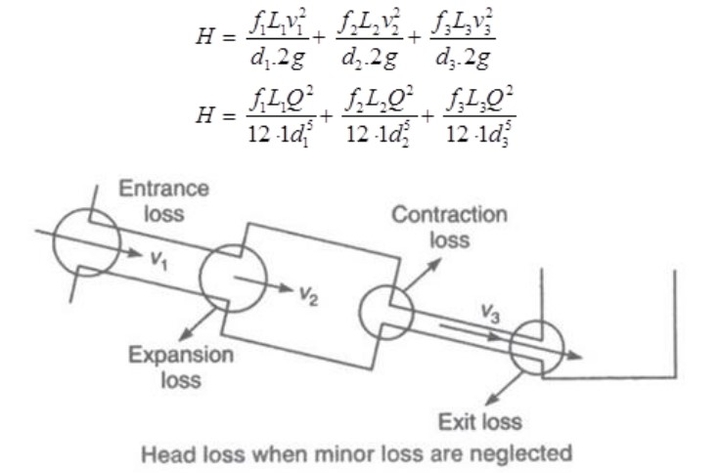
Pipe in Series: As pipes are in series, the discharge through each pipe will be the same.

Q = A₁v₁ = A₂v₂ = A₃v₃

Total loss of head = Major loss + Minor loss

H = h_L1 + h_L2

Major loss = Head loss

due to friction in each pipe

h_L1 = h_f1 + h_f2 + h_f3

While, minor loss = Entrance loss + Expansion loss + Contraction loss + Exit loss

If minor losses are neglected, then,

Pipes in Parallel: In this, discharge in the main pipe is equal to the sum of discharge in each parallel pipe.

Hence, Q = Q₁ + Q₂

The head loss in each parallel pipe is the same,

h_f1 = h_f2

where h_f1 and h_f2 are head loss at 1 and 2, respectively.

Equivalent Pipe: A compound pipe with several pipes of different lengths and diameters to be replaced by a pipe with a uniform diameter and the same length as a compound pipe is called an equivalent pipe.

(where, L = L₁ + L₂ + L₃)

If f = f₁ = f₂ = f₃

Then,

Hydraulic Gradient Line (HGL) and Total Energy Line (TEL)

HGL → It joins the piezometric head ((p/ρg) + z) at various points.

TEL → It joins the total energy head at various points:

{((p/ρg) + z) + (v²/2g)}

Note: HGL is always parallel but lower than TEL.

Power Transmission Through Pipe (P)

When a pipe is connected to a water tank, Power applied by a pipe flow at the outlet end depends upon the flow characteristics, pipe characteristics, etc. It will be explained below in detail for different cases.

P_ideal = ρgQH

P_actual = ρgQ(H - h_f); h_f = head loss

Efficiency, η = (H - h_f)/H

Power delivered by a given pipeline is maximum when the flow is such that one-third of the static head is consumed in pipe friction. Thus, efficiency is limited to only 66.66%

Maximum efficiency, η_max = H/3.

Water Hammer: When a liquid is flowing through a long pipe fitted with a vale at the end of the pipe, and the valve is closed, suddenly, a pressure wave of high intensity is produced behind the valve. This high-intensity pressure wave has the effect of hammering action on the walls of the pipe. This phenomenon is known as a water hammer.

The intensity of pressure rise due to the water hammer

P = -ρLν/t

When the valve is closed gradually, when valve closes suddenly with a rigid pipe.

P = ν × (Kρ)^0.5

When the valve closed suddenly with a plastic pipe

ρ = ν ×[ρ/{(1/K) + (D/Et)}]^0.5

If the time required to close the valve

t > 2L/C ⇒ Valve closure is said to be gradual.

t < 2L/C ⇒ The valve closure is said to be sudden.

Where,

L = Length of pipe
D = Diameter of pipe
C = Velocity of pressure wave produced due to water hammer = √(K/P)
v = Velocity of flow
K = Bulk modulus of water
E = Modulus of elasticity for pipe material.
t = Time required to choose the valve.

Other Important GATE Notes
Steel	Zero Force Member In A Truss
Functions Of The Network Layer	SHM
Geometric Design Of Highways	Moment Area Method
Macaulay's Method	Impact Load
Impulse An Momentum	Uniformly Varying Load

Daily GATE & ESE Live Sessions, Free Live Classes, Study Notes, Quizzes & Free PDF's & more, Join our Telegram Group Join Now

Flow Through Pipes FAQs

What do you mean by flow through pipes?

Flow through pipes means the study of the flow characteristics when it occurs in a pipe. During the flow through pipes, an external source of energy is always required to flow because in such conditions flow is occurring under the energy gradient.

Which type of flow is possible during the flow through pipes?

During the flow through pipes, flow can be laminar type, turbulent type, or transition type of flow. These flows can be classified based on the Reynolds number of the flow, which depends on the flow and pipe characteristics.

What are the different types of losses occured in the flow through pipes?