Fixed Beam
By BYJU'S Exam Prep
Updated on: September 25th, 2023

A fixed beam is supported by two fixed supports on both ends. It is also called a restrained beam. In a fixed beam, there are more support reactions than in equilibrium equations.
It is a fixed beam that can take more load than the simply supported beam for the same amount of deflection. It is stronger than the simply supported beam due to redundant reactions in the fixed beams. Here we have discussed in detail the fixed beam in the sections below.
Download Strength of Material Short Notes/ Formulae
Table of content
What is a Fixed Beam?
A fixed beam is a beam that is restrained with a fixed support at both ends. Fixed beams are used in the structure because it has many advantages over conventional beams. It is an indeterminate beam because it has more than one redundant reaction.
A fixed beam provides extra stability to the structure. Hence, it makes the structure stiffer and more stable. Such beams are used to withstand horizontal and vertical loading on the structure.
Download Structural Analysis Study Notes/ Formulae
Advantages of Fixed Beam
Fixed beams have many advantages over simply supported beams. Here some advantages are mentioned.
- It has more load capacity than the simply supported beam for the same loading condition.
- It has a lesser value of maximum deflection than that for a simply supported beam.
- It is subjected to a lesser maximum bending moment than that for a simply supported beam.
- The slope of fixed beams at both ends is zero.
Deflection in Fixed Beam
In a fixed beam, deflection is an important parameter to define the loading capacity of the beam. The deflection of such a beam depends upon the type of loading and distribution of load over the beam. The deflection of the beam also depends on the beam’s cross-sectional properties and material properties.
Deflection of fixed beams under the uniformly distributed load-
Bending Moment Formula For Fixed Beams
Fixed beam bending moment is a design parameter representing the beam’s overall flexural strength. The bending moment is the resistance offered by the beam against its rotation about the longitudinal axis.
Bending moment for fixed beam in case of uniformly distributed load-
What is the Degree of Indeterminacy of Fixed Beams?
As we know that fixed beams are supported with a fixed support at both ends, and we also know that fixed support has three numbers of reactions in general. These reactions include a one-moment reaction, one horizontal reaction, and one vertical reaction.
The degree of indeterminacy is the excess number of reactions not found with the number of equilibrium equations. So, for inclined loading, the Degree of Indeterminacy is (3+3)-3=3 and for vertical loading Degree of Indeterminacy is (2+2)-2=2.
Compatibility Conditions In Fixed Beams
To understand the parameter, Indeterminate beam Compatibility equations is used. Compatibility conditions of fixed beams are those equations essential for solving unknowns of the beam; these conditions consider the displacement equilibrium of the beam or structure. Compatibility simply means that there should not be deflection in more than one direction at a particular joint in an indeterminate structure.
Compatibility conditions in fixed beams are used to solve the deflection parameter of the beam. These equations involve displacement and slope equations at any beam point. These equations are based on the criteria of slope at the fixed support of the beam and deflection at the restrained supports is zero.
Fixed Beams with an Internal Hinge
Fixed Beam is a beam supported at both ends with fixed support. Hence, it is so called an indeterminate beam. An indeterminate beam is a beam that has a degree of determinacy of more than one. An internal hinge is a simple hinge provided at the beam’s central location. The internal hinge provides free rotation of the beam about the point where it is located.
The internal hinge in the fixed beam provides an extra compatibility equation; with this help, one more reaction can be found in the beam. So, the internal hinge reduces the beam’s indeterminacy by decreasing the beam’s redundant reaction.
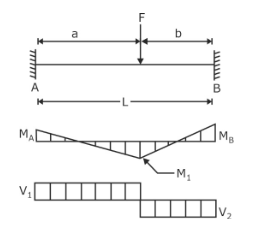
SFD and BMD For Fixed Beams
SFD and BMD for a fixed beam are a shear force diagram and bending moment diagram, respectively, along the length of the beam. SFD and BMD for fixed beams will depend on the load variation along the length of the beam. The shape of SFD and BMD depends on the loading condition and type of loading over the beam.