Dijkstra Algorithm

What is the Dijkstra Algorithm?

The single-source shortest path issue for a directed graph G = (V, E) with non-negative edge weights is solved by the greedy algorithm known as the Dijkstra algorithm, which bears the name of its discoverer, Dutch computer scientist Edsger Dijkstra. In other words, we suppose that for any edge (u, v) є E, w(u, v) ≥ 0.

The Dijkstra algorithm maintains a collection of S vertices with predetermined final shortest-path weights from the source. The procedure continually chooses the vertex u є V-S with the least shortest path estimate, inserts u into S, and relaxes all edges leaving u. In other words, all vertices in S have d[v] = 8(s, v). All the vertices in V-S are kept in a min-priority queue Q that is keyed by their d values. Adjacency lists are used to represent Graph G.

Pseudocode of Dijkstra Algorithm

Every vertex’s route distance must be preserved. That can be kept in a v-dimensional array, where v is the total number of vertices. Not only do we want to know how long the shortest path is, but we also want to be able to find it. Each vertex is mapped to the vertex that most recently changed its path length for this purpose.

When the process is finished, we can move backward to find the path by going from the source vertex to the destination vertex. The vertex with the shortest path distance can be efficiently received using a minimal priority queue.

The pseudocode of Dijkstra algorithm is as follows:

DIJKSTRA (G, w, s)
INITIALIZE-SINGLE-SOURCE (G, s)
S ← Ø
Q ← V[G]
while Q ≠ Ø
do u ← EXTRACT-MIN (Q)
S ← S ∪ (u)
for each vertex v є Adj[u]
do RELAX (u, v, w)

Analysis of Dijkstra Algorithm

The Big-O notation can be used to define the running time of the Dijkstra algorithm as a function of |E| and |V| on a graph with edges and vertices. The Dijkstra algorithm can be implemented in several ways. Still, its basic form stores Q’s vertices in an ordinary linked list or array, and operation Extract-Min (Q) is just a linear search through all of Q’s vertices. The running time in this context is O(|V|²+ |E|) = O(V²).

Dijkstra algorithm can be implemented more effectively for sparse graphs, or graphs with much fewer edges than |V|², by storing the graph as adjacency lists and utilizing a binary heap or Fibonacci heap as the priority queue to implement the Extract-Min function. When using a binary heap, the algorithm takes O((| E| |V|) time, which is dominated by O(|E| log |V|) when every vertex is assumed to be connected. The Fibonacci heap reduces this time to O(|E| + |V| log |V]).

Example of Dijkstra Algorithm

Consider the directed graph: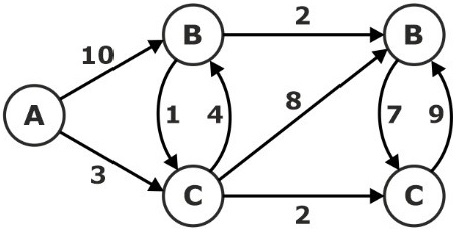

Find the shortest path from the source vertex A to the other vertices using the Dijkstra algorithm.

Solution:

Dijkstra algorithm maintains a group of S of vertices whose final shortest-path weights from the source have already been determined. The Dijkstra algorithm repeatedly selects the vertex u є V-S with the minimum shortest-path estimate, inserts u into S, and relaxes all edges leaving u. We maintain a min-priority queue Q that contains all the vertices in V – S keyed by their d values.

Initialize: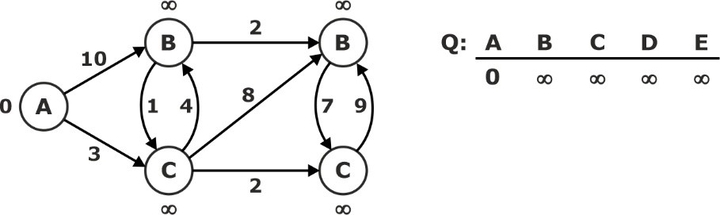

‘A’ ← EXTRACT-MIN (Q):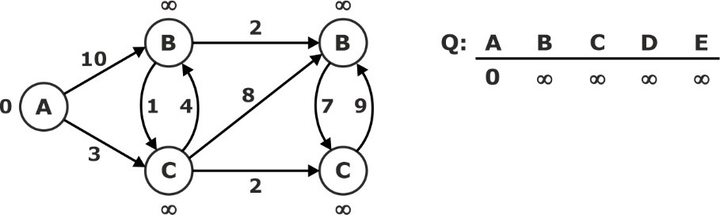

Relax all edges Leaving ‘A’ S: {A}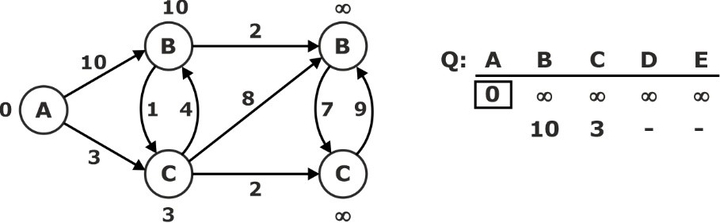

‘C’ ← EXTRACT-MIN(Q):

Relax all edges Leaving ‘A’ S: {A, C}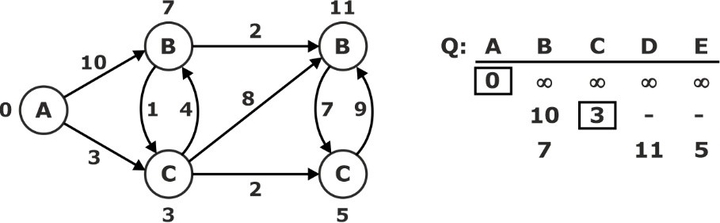

‘E’ ← EXTRACT-MIN (Q):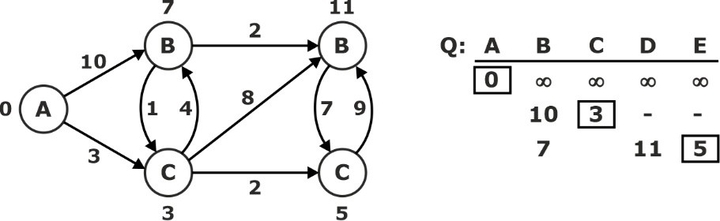

Relax all edges Leaving ‘A’ S: {A, C, E}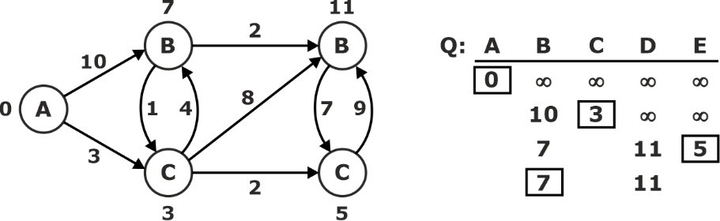

‘B’ ← EXTRACT-MIN (Q):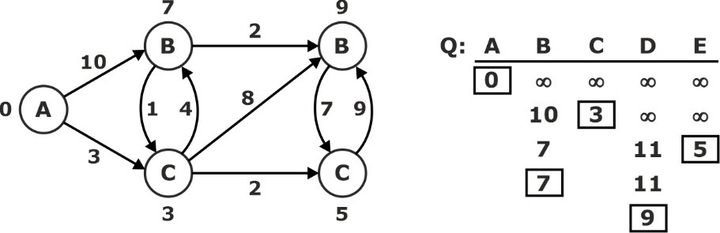

Relax all, Leaving’ A’ S: {A, C, E, B}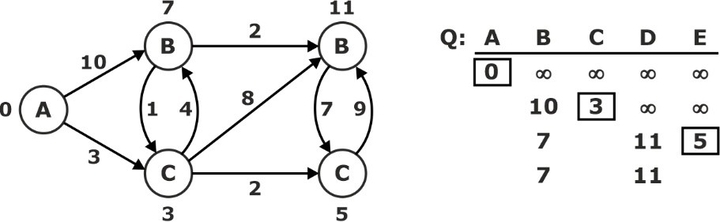

‘D’ ← EXTRACT-MIN (Q):

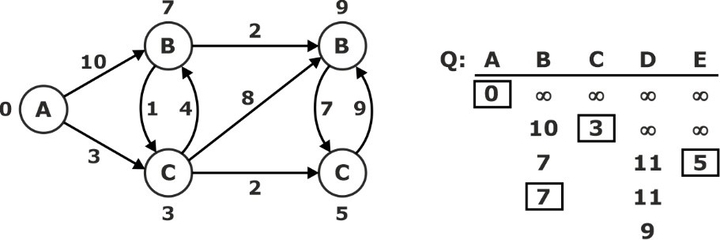
S: {A, C, E, B, D}

GATE Computer Science Engineering Revision Sheet and Formulae

Check –  Click Here to check your GATE 2023 Rank Predictor Tool

Important GATE Topics
Fixed End Moment	Gravity Of Earth
Slope Deflection Equation	Capacitors in Parallel
Capacitors in Series	Carnot Cycle
Cement Test	Clamping Circuit
CMOS Converter	Column Base