Determinate and Indeterminate Structures
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Determinate and Indeterminate Structures come under structural engineering, the branch of civil engineering in which discussions about structures have been made. The degree of indeterminacy of determinate and indeterminate structures depends on the type of support used. A structure can be classified as stable or unstable based on the determinacy of the system of its members. An unstable structure is also known as a mechanism whose degree of determinacy will be less than zero.
Indeterminacy is the number of restraints the structure offers more than the number of equilibrium equations for that particular structure. Equilibrium equations involve horizontal equilibrium, vertical equilibrium, and rotational stability. Based on the available equilibrium equations degree of indeterminacy of a determinate and indeterminate structure can be calculated. These are the key parameters that govern the stability of whole structures. Here we will see determinate and indeterminate structures in detail, along with some important terms, differences, and a few examples.
Download Complete Structural Analysis PDF
Download Formulas for GATE Civil Engineering – Solid Mechanics
Table of content
-
1.
What are Determinate and Indeterminate Structures?
-
2.
Statically Determinate and Indeterminate Structures
-
3.
Difference Between Statically Determinate and Indeterminate Structures
-
4.
Terms in Determinate and Indeterminate Structures
-
5.
What is the Degree of Indeterminacy?
-
6.
Examples of Determinate and Indeterminate Structures
What are Determinate and Indeterminate Structures?
A determinate structure is a stable structure, and all support reactions can be calculated with the help of equilibrium equations only. And there is no need for compatibility conditions in the determinate structure. The bending moment and shear force of a determinate structure is independent of the material property, while it will depend on the case of an indeterminate structure.
An indeterminate structure is a structure that is also stable, but It has more unknown forces than the total number of available equilibrium equations. For analyzing an indeterminate structure, compatibility equations are required along with the equilibrium equations. Compatibility equations may be a deformation equation, slope equation, etc.
Statically Determinate and Indeterminate Structures
Statically Determinate Structures
These structures can analyze with the help of equilibrium equations alone without any help of compatibility equations.
Statically Indeterminate Structures
These are the structures for which compatibility conditions and equilibrium equations are required for their analysis. Both determinate and indeterminate structures are stable. An indeterminate structure is stable until all degree of indeterminacy is less than zero.
Download Formulas for GATE Civil Engineering – Fluid Mechanics
Difference Between Statically Determinate and Indeterminate Structures
The indeterminacy and stability of a structure will depend upon whether the structure is determinate or indeterminate, so it will be important to understand the difference between them. A statically determinate structure is stable and can be determined from equilibrium equations alone. However, a statically indeterminate structure has more unknown forces than available equilibrium equations.
Only equilibrium equations are required to analyze a determinate structure, and it is sufficient to find unknowns of the member. But compatibility conditions are also required for the analysis of indeterminate structures, along with the equilibrium equations for finding the unknowns of the structure.
Download Formulas for GATE Civil Engineering – Environmental Engineering
Terms in Determinate and Indeterminate Structures
To understand the determinate and indeterminate structures, it is required to know the terms used. These terms are described below in detail.
Redundant: Indeterminate structures effectively have more unknowns than can be solved using the three equilibrium equations (or six equilibrium equations in 3D). These extra unknowns are called redundant reactions.
Determinate and Indeterminate Structures PDF
Stable/Unstable structure: A stable structure will not collapse when disturbed. Stability may also be defined as The power to recover equilibrium. In general, there are many ways that a structure may become unstable, including the buckling of compression members and yielding/rupture of members; however, for linear structural analysis, the main concern is instability caused by insufficient reaction points or poor layout of structural members.
Internally Stable: An internally stable structure would maintain its shape if all the support reactions were removed. An internally unstable structure may remain stable with sufficient external support reactions.
What is the Degree of Indeterminacy?
The degree of indeterminacy equals the number of redundant reactions available in the structure. It helps to identify the determinate and indeterminate structures. An indeterminate structure with 2 redundancies may be statically indeterminate to the second degree. The degree of indeterminacy can be either external determinacy or internal determinacy, which are explained below.
- External Determinacy: The ability to calculate all of the external reaction component forces by using only static equilibrium. A structure that satisfies this requirement is the externally statically determinate. Conversely, a structure for which the external reactions component forces cannot be calculated using only equilibrium is an externally statically indeterminate structure.
- Internal Determinacy: The ability to calculate the external reaction components and internal forces using only static equilibrium. A structure that satisfies this requirement is the internally statically determinate. A structure for which the internal forces cannot be calculated using only equilibrium is an internally statically indeterminate structure.
Examples of Determinate and Indeterminate Structures
As is already discussed that Determinate structure is a structure that does not require compatible conditions for solving their unknown forces. In contrast, in an indeterminate structure, compatibility equations along with equilibrium equations are required. Determinate and indeterminate structures can be classified based on the degree of determinacy of the structure. So let’s understand the determinate and indeterminate structures with the help of an example.
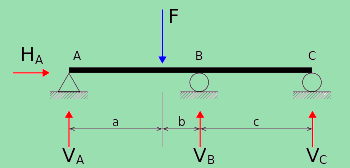
Here, in this structure, vertical loading is given over a beam. So it’s necessary to understand that in the case of vertical loading, only two equilibrium equations can be used because there is no sign of horizontal equilibrium in such cases.
So, in this case,
Total number of support reactions = 3 (i.e., VA, VB, VC)
And the total number of equilibrium equations available = 2
Hence, degree of static determinacy = 3 – 2 = 1
So, the above structure is a statically indeterminate structure of degree one.
|
Important GATE Topics |
|
| Fixed End Moment | Gravity Of Earth |
| Slope Deflection Equation | Capacitors in Parallel |
| Capacitors in Series | Carnot Cycle |
| Cement Test | Clamping Circuit |
| CMOS Converter | Column Base |


