Degree of Static Indeterminacy

What is Degree of Static Indeterminacy?

We need to know about the support reactions and equilibrium equations to calculate the degree of static indeterminacy.

Degree of Static Indeterminacy Definition

The degree of static indeterminacy is calculated by subtracting the available equilibrium equations from the total number of unknown reactions present in the structure. It also depends upon the direction of loading on the beam. So, it can be said that the degree of static determinacy will be different for the inclined loading and vertical loading acting over the same beam.

Degree of Static Indeterminacy Formula

In the case of inclined loading on the beam, three equilibrium equations will be available. Still, in the case of pure vertical loading, only two numbers of equilibrium equations will be available. As in the case of vertical loading, there will not be any signs of horizontal equilibrium. Hence the value of static determinacy changes in both cases. If we talk about a general formula for calculating the static determinacy, it will be

D_s=D_se+D_si; and D_se = R-3 (for the 2D structure)

D_se=R-6 (for the 3D structure)

where R is the number of total reactions.

Download Formulas for GATE Civil Engineering – Environmental Engineering

Degree of Static Indeterminacy of Beams

Any structure can calculate static indeterminacy by adding external and internal static indeterminacy. But in the case of beams, internal static indeterminacy is equal to zero. Hence, the degree of static indeterminacy of beams is equal to the external static indeterminacy only, which can be calculated by the sum of all the redundant reactions in the beam.

Degree of Static Indeterminacy of a Fixed Beam

In the case of a fixed beam, there will be fixed supports at both ends of the beam. If a fixed beam has an inclined loading over it, then the degree of static indeterminacy will be 6 – 3 = 3. But if a fixed beam has only vertical loading over it, then, in this case, the degree of static indeterminacy will be 4 – 2 = 2.

Degree of Static Indeterminacy of Propped Cantilever

The degree of static indeterminacy of a propped cantilever is the extra number of reactions available than the equilibrium equations in the beam. Equilibrium equations in the beam will depend upon whether the loading will be inclined or purely vertical. In the case of inclined loading on the beam, there will be three equilibrium equations. Still, in the case of vertical loading, there will be only two equilibrium equations because, in this case, the equation for horizontal equilibrium is insignificant.

Download Formulas for GATE Civil Engineering – Irrigation & Hydrology

Degree of Static Indeterminacy of Propped Cantilever Beam having Vertical loading

In the case of a propped cantilever beam, there is fixed support at one end of the beam, and a hinge supports the other end of this beam. So the total number of reactions for such a beam is 2+1=3 in the case of vertical loading. And there are only two numbers of equilibrium equations available in this beam condition. Hence, the degree of static determinacy will be 3 – 2 = 1.

Degree of Static Indeterminacy in Two-hinged Arch

For the calculation of the degree of static indeterminacy in the two hinged arches, first, we need to understand the arch. An arch is a structure that can support vertical loading as well as inclined loading. Arch may be classified as two hinged arch and three hinged arches based on the number of hinges available in the structure. In the case of two hinged arches, hinges are provided only on supports. Still, in three hinged arch structures, an additional hinge is provided in between the arch’s span, making it a determinate structure by inducing one more equilibrium equation for the structure.

So, in the case of two hinged arches, there are four numbers of support reactions, with each support consisting of two reactions, one in the horizontal direction and the other in the vertical direction. And indeterminacy can be calculated by subtracting the equilibrium equations from the total number of support reactions. Hence, the degree of static indeterminacy in two hinged arches equals 4 – 3 = 1.

Degree of Static Indeterminacy of Cantilever Beam

For the calculation of the degree of static indeterminacy of the cantilever beam, first, we need to understand the support reactions associated with the cantilever beam. The cantilever beam is a beam that has fixed support at one end, and the other end of this beam is free. So, the total number of support reactions will equal three when it is subjected to inclined loading. And there will be only two support reactions when it is subjected to vertical loading across its span.

So, a cantilever beam’s degree of static indeterminacy will be 3 – 3 = 0; when it is subjected to inclined loading on its span. And it will be equal to 2 – 2 = 0; when it is subjected to pure vertical loading on its whole span.

Degree of Static Indeterminacy of a Rigid Jointed Plane Frame

First, we need to understand the support reactions and joint structure associated with the frame to calculate the degree of static indeterminacy of a rigid joint plane frame. A rigid joint plane frame is a framed structure in which all the joints are rigidly connected. So, the movement of members occurred simultaneously. Here an example of a rigid jointed plane frame is shown below.

Degree of Static Indeterminacy Solved Question

Question: What will be the degree of indeterminacy of the frame showing the figure

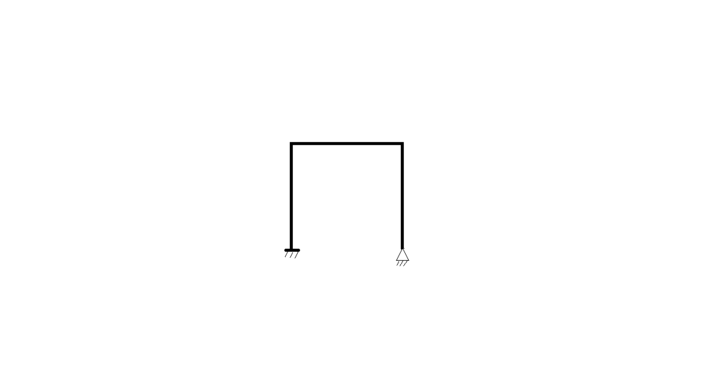
Solution:

Here, in this framed structure

Total number of members m=3, Total number of joints j=4, Total number of reactions r=3+2=5.

So the degree of static indeterminacy D_S=D_Se+D_Si

And, D_Se=R-3=5-3=2, D_Si=0.

So, D_S=2

Related Important Links

Important GATE Topics
Lan Full Form	Propped Cantilever Beam
Torsional Force	POP Full Form
RTC Full Form	Fcfs Scheduling Full Form
Types Of Loads	E-Commerce Mcq
Laser Full Form	Rankine Formula