CDS Algebra Questions - PDF, Tips to Solve Algebra Questions

Important Topics for CDS Algebra Questions

In CDS Algebra Questions, symbols are used, and operators are used to connect the symbols to one another. It is more than just a mathematical idea; it is a skill that we all utilize on a regular basis without even being aware of it. The following are the topics covered under CDS Algebra questions:

• Basic Operations, simple factors, Remainder Theorem.
• Theory of polynomials, Solutions of quadratic equations, relation between its roots and coefficients.
• Simultaneous linear equations in two unknowns-analytical and graphical solutions. Simultaneous linear equations in two variables and their solutions.
• Practical problems leading to two simultaneous linear equations or equations in two Variables or quadratic equations in one variable & their solutions.
• Set language and set notation, rational expressions and conditional identities, and Laws of indices.

Important Formulae and Theorems for CDS Algebra Questions

The following are some important formulae and theorems for Algebra questions for CDS Exam:

1. a² – b² = (a – b)(a + b)
2. (a + b)² = a² + 2ab + b² 
3. a² +b²  = (a – b)² + 2ab
4. (a – b)²  = a²  – 2ab + b² 
5. (a + b + c)²  = a²  + b²  + c² + 2ab + 2ac + 2bc
6. (a + b + c)³  = a³  + b³ + c³ + 3(a + b)(b + c)(c + a)
7. a³ + b³ + c³ - 3abc = (a + b+ c) ( a² + b² + c² - ab - ac - bc) = 12(a+b+c) [(a-b)² + (b-c)² + (c-a)² ]
   if (a+b+c) = 0, then a³ + b³ + c³ = 3abc
8. (a + b)³ = a³ + 3a²b + 3ab² + b³ ;
   or, (a + b)³ = a³ + b³ + 3ab(a + b)
9. (a – b)³ = a³ – 3a²b + 3ab² – b³
   
10.  a³ – b³ = (a – b)(a² + ab + b²)
11. a³ + b³ = (a + b)(a² - ab + b²)
12. x²+ x(a + b) + ab = (x + a) (x + b)
13. Rules of indices
    • a^-n = 1/aⁿ
    • (a^m)(aⁿ) = a^m+n
    • (ab)^m = a^mb^m
    • (a^m)ⁿ = a^mn
    • a^m/aⁿ = am^-n
    • a⁰ = 1
14. Remainder Theorem – Let f(x) be a polynomial of a degree greater than or equal to one and α be any real number, if f(x) is divided by (x-α) then the remainder is f(α).
15. Factor theorem – Let f(x) be a polynomial of degree greater than or equal to one and α be any real number such that f(α) = 0, then (x-α) is a factor of f(x).
16. Relation between roots and coefficients of a quadratic equation
17. A quadratic equation is of the form ax²+bx+c = 0, where a, b and c are real numbers and a≠0. Let α and β be the roots of the quadratic equation, then
    Sum of roots i.e. (α+β) = -b/a, and
    Product of roots i.e. αβ = c/a, and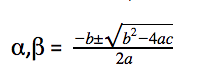
    

Tips and Tricks for Solving CDS Algebra Questions

Here are some tips and strategies for addressing CDS Algebra questions:

• A lot of CDS Algebra questions can be solved by putting some values of variables in the question, and it can help you in solving the question in no time. But this method needs to be applied very carefully. Your first approach to solving the problem should always be through basic methods especially when you are practicing at home.
• Even if you solve a problem correctly by putting values in variables, you must be aware of the basic method to solve the question. So after solving questions in quizzes you must look for basic/alternative methods in the solutions provided.
• Variety of questions in algebra is more as compared to other topics in mathematics. In order to solve CDS Algebra questions easily in the exam you should be familiar with the different types of questions that are asked in the exam. If you would have solved similar questions before, it will be quite easy for you to attempt them in the exam. So we sincerely advise you to solve the previous year's question papers of at least 5 years before appearing in the exam.
• You must remember all the important formulae for CDS Algebra questions. There is just no way around it.

To give you some idea about the type of CDS Algebra questions asked in the exam, here are some questions asked in the previous exams.

1. If x = y^1/a, y = z^1/b, and z = x^1/c where x≠1, y≠1, z≠1, then what is the value of abc?

1. -1
2. 1
3. 0
4. 3

Solution:

x = y^1/a, y = z^1/b, and z = x^1/c

Taking log in the above given equations,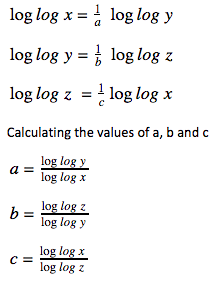

2. If the roots of the equation px² + x + r = 0 are reciprocal to each other, then which one of the following is correct?

1. P = 2r
2. P = r
3. 2p = r
4. P = 4r

Solution:

Let the roots be x and 1/x.

Use the property of quadratic equations {x+y = -b/a , xy = c/a};
x*1/x = r/p
1 = r/p
r = p
Thus option (b) is correct.

3. What is the value of α (α≠0) for which x² - 5x + α and x² - 7x + 2α have a common factor?

1. 6
2. 4
3. 3
4. 2

Solution:

Let (x - a) be the factor of both quadratic equation.
i.e. x = a is the root of both equation. Then x = a will satisfy both the equation.
So, a² - 5a + a = 0... (i) and
a² - 7a + 2a = 0... (ii)
Using quadratic formula for both (i) and (ii), we get: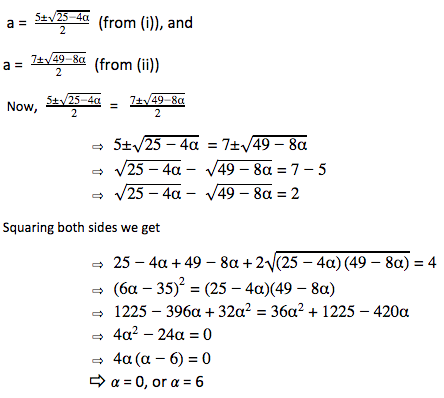

Thus option (a) is the correct answer.

Lastly, practicing previous year's papers and solving CDS Mock Tests would benefit the candidate in scoring good marks in the exam.

Also, check:

• CDS Syllabus
• CDS Exam Analysis
• CDS Exam Pattern
• CDS Previous Year Question Paper