- Home/
- CDS & Defence/
- Article
A particle is moving along a straight line with uniform acceleration has velocities 7m/s at P and 17m/s at Q if R is the midpoint of PQ then average velocity between R and Q is.
By BYJU'S Exam Prep
Updated on: September 25th, 2023
The average velocity is 15 m/s. The average velocity is defined as the difference between the change in location or displacement (∆x) and the time intervals (∆t) during which the change occurs. Depending on the direction of the displacement, average velocity is a vector quantity that can be positive or negative. The SI unit for average velocity is meters per second (m/s or ms-1).
The incidence of any single object’s displacement from its original position over a certain period of time is another way to quantify average velocity. Additionally, average velocity is the term used to describe the proportion of an object’s entire displacement to its total travel duration.
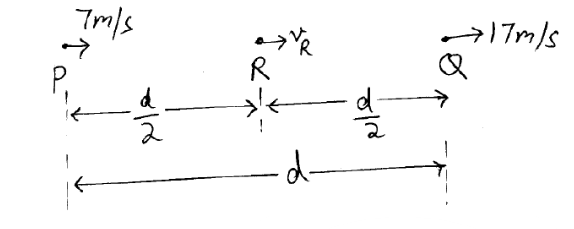
According to the question we can write as:
VQ2 = VP2 + 2a (d)
Substituting the values we get:
172 = 72 + 2a (d)
On rearranging we get:
a = (289 – 49)/2d
a = 120/d
We have:
VQ2 = VR2 + 2a (d/2)
On rearranging we get:
VR2 = VQ2 – 2a (d/2)
Substituting the values we get:
= 172 – 2 (120/d) (d/2) = 289 – 120
= 169
VR = 13 m/s
VQ = VR + at
17 = 13 + 120/d tRQ
4 = 120/d tRQ
tRQ = d/30
The average velocity between R and Q is:
Vav = (d/2)/tRQ
In simplification we get the:
Vav = 15 m/s
Summary:
A particle is moving along a straight line with uniform acceleration has velocities 7m/s at P and 17m/s at Q if R is the midpoint of PQ then average velocity between R and Q is.
A particle moving along a straight line with uniform acceleration has velocities 7m/s at P and 17m/s at Q if R is the midpoint of PQ then the average velocity between R and Q is 15 m/s.
