A ball is thrown vertically upwards with a velocity of 20m/s² from the top of a multi-storey building. The height of the point from where the ball is thrown is 25m from the ground. (a) How high will the ball rise (b) How long will it be before the ball hits the ground? Take g=10m/s

By BYJU'S Exam Prep

Updated on: September 25th, 2023

The ball will rise at 45 cm. It will be 5s before the ball hits the ground. Steps to calculate How high will the ball rise and How long will it be before the ball hits the ground.

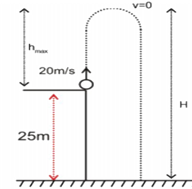
How high will the ball rise

Here u = 20m/s. When its velocity along y becomes zero, the height it will go corresponds to the distance h from the tower, that is v = 0

We have:

v² = u² – 2gh

We know that v = 0

u² – 2gh = 0

h = u²/2gh = (20)²/(2 x 10) = 20 m

Height from the ground = 20 + 25 = 45 cm.

Table of content

1. A ball is thrown vertically upwards with a velocity of 20m/s² from the top of a multi-storey building. The height of the point from where the ball is thrown is 25m from the ground. (a) How high will the ball rise (b) How long will it be before the ball hits the ground? Take g=10m/s

The ball’s time in the air (T) will be equal to its displacement from the ground, which will be zero.

y = 0
t = T

Displacement in the y direction is given by:

y = y0 + ut – ½ gt2

y = 0, t = T

Substituting the values we get:

25 + 20 x T – ½ x 10 x T2 = 0

T2 – 4T – 5 = 0

Simplifying we get:

Either T = 5 or T = -1

Time cannot be negative so: T = 5 s

Summary: